题目内容
(本小题满分12分)设数列{an}的前n项和为Sn,对任意的正整数n,都有an=4Sn+1成立.
(1)求数列{an}的通项公式;
(2)设bn=log3|an|,数列{ }的前n项和为Tn, 求证:Tn<
}的前n项和为Tn, 求证:Tn< .
.
(1) ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)由已知,计算a1=4S1+1a1=-
又由 得an+1-an=4an+1
得an+1-an=4an+1
推出数列{an}是首项为- ,公比为-
,公比为- 的等比数列.
的等比数列.
(2)由bn=log3|an|=log3|(- )n|=n
)n|=n
得到 ,利用“裂项相消法”计算得
,利用“裂项相消法”计算得

 (1+
(1+ ―
― ―
― )“放大”即得证.
)“放大”即得证.
试题解析:(1)当n=1时,a1=4S1+1a1=-
又由 得an+1-an=4an+1
得an+1-an=4an+1
∴ =-
=- (n∈N*) 4分
(n∈N*) 4分
即数列{an}是首项为- ,公比为-
,公比为- 的等比数列,
的等比数列,
∴an=(- )n, (n∈N*) 6分
)n, (n∈N*) 6分
(2)∵bn=log3|an|=log3|(- )n|=n
)n|=n
∴ 8分
8分
∴Tn= [(1-
[(1- )+(
)+( -
- )+(
)+( -
- )+ +(
)+ +( -
- )]
)]
= (1+
(1+ ―
― ―
― )<
)< ·
· =
= 12分
12分
考点:1.等比数列;2.数列的求和、“裂项相消法”.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 ,a=10,b=7,则该三角形有且有两解;②若三角形的三边的比是3:5:7,则此三角形的最大角为120
,a=10,b=7,则该三角形有且有两解;②若三角形的三边的比是3:5:7,则此三角形的最大角为120 的取值范围是
的取值范围是 .其中正确命题的个数是 ( )
.其中正确命题的个数是 ( ) ,
, ,则
,则 =( ).
=( ). B.
B. C.
C. D.
D. 
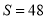 ,则输入
,则输入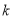 的值可以为( ).
的值可以为( ).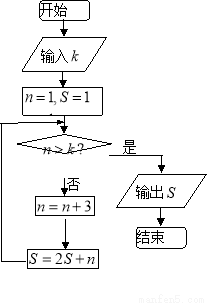
 B.
B.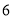 C.
C. D.
D.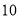

 ;
; 则z=x+2y的取值范围是( )
则z=x+2y的取值范围是( )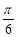 ] B.[0,
] B.[0, 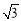 ] C.[0,
] C.[0,  上有一点P,F1, F2是椭圆的左、右焦点,若△F1PF2为直角三角形,则这样的点P有( )
上有一点P,F1, F2是椭圆的左、右焦点,若△F1PF2为直角三角形,则这样的点P有( )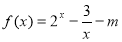 的一个零点在区间(1,3)内,则实数
的一个零点在区间(1,3)内,则实数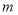 的取值范围是
的取值范围是 的共轭复数是
的共轭复数是 B.
B.  C.
C.  D.
D. 