题目内容
13.利用定积分的定义求由直线x=1,x=2,y=0与曲线y=x3围成的图形的面积.分析 利用分割、近似代替、求和、求极限的方法,即可得出结论.
解答  解:(1)分割
解:(1)分割
如图,把曲边梯形ABCD分割成n个小曲边梯形,用分点$\frac{n+1}{n}$.$\frac{n+2}{n}$,…$\frac{n+(n-1)}{n}$把区间[1,2]等分成n个小区间,每个小区间的长度为△x=$\frac{1}{n}$,过各分点作x轴的垂线,把曲边梯形ABCD分割成n个小曲边梯形,它们的面积分别记作△S1,△S2,…,△Sn.
(2)近似代替取各小区间的左端点ξi,用以点ξi的纵坐标ξi3为一边,以小区间长△x=$\frac{1}{n}$为其邻边的小矩形面积近似代替第i个小曲边梯形面积,可以近似地表示为
△Si≈ξi3•△x=$(\frac{n+i-1}{n})^{3}•\frac{1}{n}$(i=1,2,3,…,n).
(3)求和
因为每一个小矩形的面积都可以作为相应的小曲边梯形面积的近似值,所以n个小矩形面积的和就是曲边梯形ABCD面积S的近似值,即S=$\sum_{i=1}^{n}△{S}_{i}$=$\sum_{i=1}^{n}$$(\frac{n+i-1}{n})^{3}•\frac{1}{n}$ ①
(4)求极限
当分点数目愈多,即△x愈小时,和式①的值就愈接近曲边梯形ABCD的面积S.因此,n→∞即△x→0时,和式①的极限就是所求的曲边梯形ABCD的面积.
$\sum_{i=1}^{n}$$(\frac{n+i-1}{n})^{3}•\frac{1}{n}$=$\frac{1}{{n}^{4}}$•$\sum_{i=1}^{n}$(n+i-1)3
=$\frac{1}{{n}^{4}}$•[n(n-1)3+3(n-1)2•$\frac{n(n+1)}{2}$+3(n-1)•$\frac{n}{6}$(n+1)(2n+1)+$\frac{1}{4}{n}^{2}(n+1)^{2}$,
∴S=$\underset{lim}{n→∞}$$\sum_{i=1}^{n}$$(\frac{n+i-1}{n})^{3}•\frac{1}{n}$=1+$\frac{3}{2}$+1+$\frac{1}{4}$=$\frac{15}{4}$.
点评 本题考查利用定积分的定义求面积,考查学生分析解决问题的能力,属于中档题.

| A. | 总有MP+OM>1 | B. | 总有MP+OM=1 | ||
| C. | 存在角α,使MP+OM=1 | D. | 不存在角α,使MP+OM<0 |
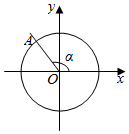 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
| A. | $\frac{11}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -1 |