题目内容
函数y=kx(k>0)的图象与函数y=log2x的图象交于两点A1、B1(A1在线段OB1上,O为坐标原点),过A1、B1作x轴的垂线,垂足分别为M、N,并且A1M、B1N分别交函数y=log4x的图象于A2、B2两点.
(1)试探究线段A1A2、A2M的大小关系;
(2)若A1B2平行于x轴,求四边形A1A2B2B1的面积.
(1)试探究线段A1A2、A2M的大小关系;
(2)若A1B2平行于x轴,求四边形A1A2B2B1的面积.
分析:(1)设A1(x1,log2x1),B1(x2,log2x2),则A2(x1,log4x1),B2(x2,log4x2),由题意可求得A1A2=
log2x1,A2M=
log2x1,从而可得答案;
(2)若A1B2平行于x轴,可求得
,从而可求得
,得到A1,B1,,A2,B2的坐标,从而可求四边形A1A2B2B1的面积.
| 1 |
| 2 |
| 1 |
| 2 |
(2)若A1B2平行于x轴,可求得
|
|
解答:解:由题设A1(x1,log2x1),B1(x2,log2x2),则A2(x1,log4x1),B2(x2,log4x2),
(1)A1A2=log2x1-log4x1=log2x1-
log2x1=
log2x1;
A2M=log4x1=
log2x1,
故A1A2=A2M;
(2)若A1B2平行于x轴,则log2x1=log4x2=
log2x2=log2
,x1=
;
又log2x1=kx1,log2x2=kx2,
联立方程组
,解得
此时A1(2,1),B1(4,2),A2(2,
),B2(4,1).
∴四边形A1A2B2B1的面积=
=
.
(1)A1A2=log2x1-log4x1=log2x1-
| 1 |
| 2 |
| 1 |
| 2 |
A2M=log4x1=
| 1 |
| 2 |
故A1A2=A2M;
(2)若A1B2平行于x轴,则log2x1=log4x2=
| 1 |
| 2 |
| x2 |
| x2 |
又log2x1=kx1,log2x2=kx2,
联立方程组
|
|
此时A1(2,1),B1(4,2),A2(2,
| 1 |
| 2 |
∴四边形A1A2B2B1的面积=
(
| ||
| 2 |
| 3 |
| 2 |
点评:本题考查对数的运算性质,考查解方程组的能力,考出转化思想与方程思想的运用,考查思维与运算能力,属于难题.

练习册系列答案
相关题目
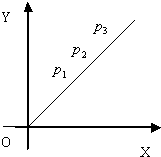 如图,在正比例函数y=kx(k>0)图象上有一列点P1,P2,P3,P4,…,Pn,….已知n≥2时,
如图,在正比例函数y=kx(k>0)图象上有一列点P1,P2,P3,P4,…,Pn,….已知n≥2时,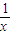 (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图象的交点为A,与x轴的交点为B,设点P的横坐标为t,A、B的横坐标分别为xA、xB,记f(t)=xA•xB.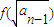 (n≥2),数列{bn}满足bn=
(n≥2),数列{bn}满足bn=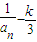 ,求an与bn;
,求an与bn; .
.