题目内容
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
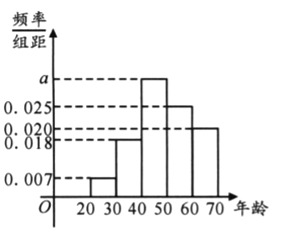
名作为样本进行分析,按年龄段![]() 分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
年龄 (单位:岁) |
|
|
|
|
|
保费 (单位:元) |
|
|
|
|
|
(1)用样本的频率分布估计总体分布,为使公司不亏本,求![]() 精确到整数时的最小值
精确到整数时的最小值![]() ;
;
(2)经调查,年龄在![]() 之间老人每
之间老人每![]() 人中有
人中有![]() 人患该项疾病(以此频率作为概率).该病的治疗费为
人患该项疾病(以此频率作为概率).该病的治疗费为![]() 元,如果参保,保险公司补贴治疗费
元,如果参保,保险公司补贴治疗费![]() 元.某老人年龄
元.某老人年龄![]() 岁,若购买该项保险(
岁,若购买该项保险(![]() 取
取![]() 中的
中的![]() ).针对此疾病所支付的费用为
).针对此疾病所支付的费用为![]() 元;若没有购买该项保险,针对此疾病所支付的费用为
元;若没有购买该项保险,针对此疾病所支付的费用为![]() 元.试比较
元.试比较![]() 和
和![]() 的期望值大小,并判断该老人购买此项保险是否划算?
的期望值大小,并判断该老人购买此项保险是否划算?
【答案】(1)30;(2)![]() ,比较划算.
,比较划算.
【解析】
(1)由频率和为1求出![]() ,根据
,根据![]() 的值求出保费的平均值
的值求出保费的平均值![]() ,然后解一元一次不等式
,然后解一元一次不等式![]() 即可求出结果,最后取近似值即可;
即可求出结果,最后取近似值即可;
(2)分别计算参保与不参保时的期望![]() ,
,![]() ,比较大小即可.
,比较大小即可.
解:(1)由![]() ,
,
解得![]() .
.
保险公司每年收取的保费为:
![]()
∴要使公司不亏本,则![]() ,即
,即![]()
解得![]()
∴![]() .
.
(2)①若该老人购买了此项保险,则![]() 的取值为
的取值为![]()
![]()
∴![]() (元).
(元).
②若该老人没有购买此项保险,则![]() 的取值为
的取值为![]() .
.
![]()
∴![]() (元).
(元).
![]()
∴年龄为![]() 的该老人购买此项保险比较划算.
的该老人购买此项保险比较划算.

【题目】某高中数学建模兴趣小组的同学为了研究所在地区男高中生的身高与体重的关系,从若干个高中男学生中抽取了1000个样本,得到如下数据.
数据一:身高在![]() (单位:
(单位:![]() )的体重频数统计
)的体重频数统计
体重 ( |
|
|
|
|
|
|
|
|
人数 | 20 | 60 | 100 | 100 | 80 | 20 | 10 | 10 |
数据二:身高所在的区间含样本的个数及部分数据
身高 |
|
|
|
|
|
平均体重
| 45 | 53.6 | 60 | 75 |
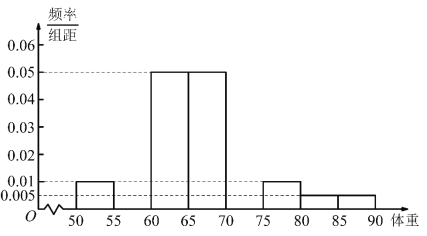
(1)依据数据一将上面男高中生身高在![]() (单位:
(单位:![]() )体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在
)体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在![]() (单位:
(单位:![]() )的中学生的平均体重;(保留小数点后一位)
)的中学生的平均体重;(保留小数点后一位)
(2)依据数据一、二,计算身高(取值为区间中点)和体重的相关系数约为0.99,能否用线性回归直线来刻画中学生身高与体重的相关关系,请说明理由;若能,求出该回归直线方程;
(3)说明残差平方和或相关指数![]() 与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
参考公式: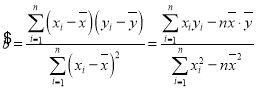 ,
,![]() .
.
参考数据:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ;(4)
;(4)![]() .
.