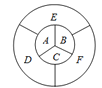
题目内容
【题目】将直角三角形![]() 沿斜边上的高
沿斜边上的高![]() 折成
折成![]() 的二面角,已知直角边
的二面角,已知直角边![]() ,那么下面说法正确的是_________.
,那么下面说法正确的是_________.
(1) 平面![]() 平面
平面![]() (2)四面体
(2)四面体![]() 的体积是
的体积是![]()
(3)二面角![]() 的正切值是
的正切值是![]() (4)
(4)![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]()
【答案】(3)(4)
【解析】
画出图像,由图像判断(1)是否正确;计算![]() 的体积来判断(2)是否正确;依题意建立空间直角坐标系,利用空间向量的方法判断(3),(4)是否正确.
的体积来判断(2)是否正确;依题意建立空间直角坐标系,利用空间向量的方法判断(3),(4)是否正确.
画出图像如下图所示,由图可知(1)的判断显然错误.由于![]() ,故
,故![]() 是二面角
是二面角![]() 的平面角且
的平面角且![]() 平面
平面![]() ,故
,故![]() .过
.过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,由于
,由于![]() ,故
,故![]() 是三棱锥
是三棱锥![]() 的高.在原图中,
的高.在原图中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,故(2)错误.以
,故(2)错误.以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则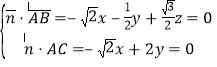 ,令
,令![]() ,则
,则![]() ,即
,即![]() .平面
.平面![]() 的法向量是
的法向量是![]() .设二面角
.设二面角![]() 的平面角为
的平面角为![]() ,由图可知
,由图可知![]() 为锐角,故
为锐角,故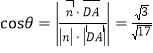 ,则其正切值为
,则其正切值为![]() .故(3)判断正确.平面
.故(3)判断正确.平面![]() 的法向量为
的法向量为![]() ,
,![]() ,设直线
,设直线![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,则
,则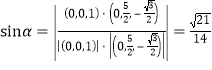 ,故(4)判断正确.综上所述,正确的有(3),(4).
,故(4)判断正确.综上所述,正确的有(3),(4).

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
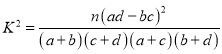 (其中
(其中 ![]() )
)