题目内容
【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”.已知椭圆![]() ,以椭圆
,以椭圆![]() 的焦点为顶点作相似椭圆
的焦点为顶点作相似椭圆![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与椭圆
两点,且与椭圆![]() 仅有一个公共点,试判断
仅有一个公共点,试判断![]() 的面积是否为定值(
的面积是否为定值(![]() 为坐标原点)?若是,求出该定值;若不是,请说明理由.
为坐标原点)?若是,求出该定值;若不是,请说明理由.
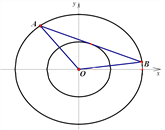
【答案】(1)![]() ;(2)6.
;(2)6.
【解析】分析:(Ⅰ)由相似椭圆的定义可得,椭圆![]() 的离心率
的离心率![]() ,由长轴的顶点为(-2,0),(2,0),于是可得
,由长轴的顶点为(-2,0),(2,0),于是可得![]() ,从而可得椭圆
,从而可得椭圆![]() 的方程;(Ⅱ)设直线
的方程;(Ⅱ)设直线![]()
![]() .
.
由 得,
得,![]() ,利用判别式为零可得
,利用判别式为零可得![]() ,联立
,联立![]() 与
与![]() ,利用韦达定理、弦长公式、点到直线距离公式以及三角形面积公式可得
,利用韦达定理、弦长公式、点到直线距离公式以及三角形面积公式可得![]() .
.
详解:(Ⅰ)由条件知,椭圆![]() 的离心率
的离心率![]() ,且长轴的顶点为(-2,0),(2,0),
,且长轴的顶点为(-2,0),(2,0),
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]()
![]() .
.
由 得,
得,![]() .
.
令![]() 得,
得,![]() .
.
联立![]() 与
与![]() ,化简得
,化简得![]() .
.
设A(![]() ),B(
),B(![]() ),则
),则
∴![]() ,而原点O到直线
,而原点O到直线![]() 的距离
的距离![]()
∴![]() .
.
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 或
或![]() ,则
,则![]() ,原点O到直线
,原点O到直线![]() 的距离
的距离![]() ,
,
∴![]() .
.
综上所述,![]() 的面积为定值6.
的面积为定值6.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
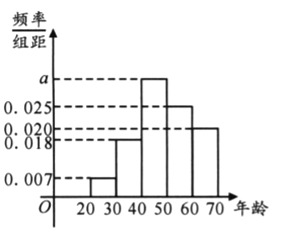
年龄 (单位:岁) |
|
|
|
|
|
保费 (单位:元) |
|
|
|
|
|
(1)用样本的频率分布估计总体分布,为使公司不亏本,求![]() 精确到整数时的最小值
精确到整数时的最小值![]() ;
;
(2)经调查,年龄在![]() 之间老人每
之间老人每![]() 人中有
人中有![]() 人患该项疾病(以此频率作为概率).该病的治疗费为
人患该项疾病(以此频率作为概率).该病的治疗费为![]() 元,如果参保,保险公司补贴治疗费
元,如果参保,保险公司补贴治疗费![]() 元.某老人年龄
元.某老人年龄![]() 岁,若购买该项保险(
岁,若购买该项保险(![]() 取
取![]() 中的
中的![]() ).针对此疾病所支付的费用为
).针对此疾病所支付的费用为![]() 元;若没有购买该项保险,针对此疾病所支付的费用为
元;若没有购买该项保险,针对此疾病所支付的费用为![]() 元.试比较
元.试比较![]() 和
和![]() 的期望值大小,并判断该老人购买此项保险是否划算?
的期望值大小,并判断该老人购买此项保险是否划算?