题目内容
(本小题满分14分)已知关于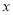 的函数
的函数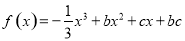 ,其导函数为
,其导函数为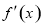 .记函数
.记函数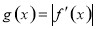 在区间
在区间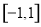 上的最大值为
上的最大值为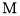 .
.
(1)如果函数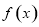 在
在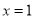 处有极值
处有极值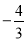 ,试确定
,试确定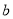 、
、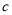 的值;
的值;
(2)若 ,证明:对任意的
,证明:对任意的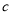 ,都有
,都有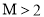 ;
;
(3)若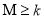 对任意的
对任意的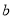 、
、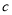 恒成立,试求
恒成立,试求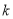 的最大值.
的最大值.
(1)b=-1,c=3;(2)见解析;(3)k的最大值为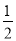
【解析】
试题分析:(1)【解析】
∵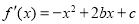
由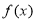 在
在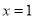 处有极值
处有极值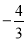 ,可得
,可得
解得,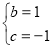 或
或 2分
2分
若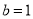 ,
,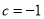 ,则
,则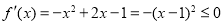 ,此时函数
,此时函数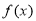 没有极值 3分
没有极值 3分
若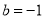 ,
,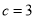 ,则
,则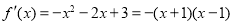
此时当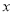 变化时,
变化时,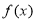 ,
,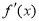 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| - |
|
|
| - |
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
∴ 当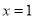 时,
时,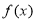 有极大值
有极大值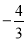
故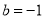 ,
,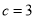 即为所求 4分
即为所求 4分
(2)证法一:
当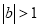 时,函数
时,函数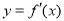 的对称轴
的对称轴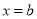 位于区间
位于区间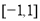 之外
之外
∴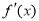 在区间
在区间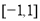 上的最值在两端点处取得,故
上的最值在两端点处取得,故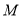 应是
应是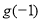 和
和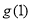 中较大的一个
中较大的一个
∴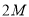
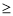
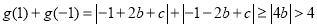 ,即
,即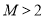 8分
8分
证法二(反证法):因为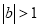 ,所以函数
,所以函数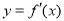 的对称轴
的对称轴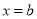 位于区间
位于区间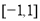 之外
之外
∴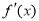 在区间
在区间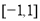 上的最值在两端点处取得,故
上的最值在两端点处取得,故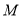 应是
应是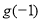 和
和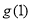 中较大的一个
中较大的一个
假设 ,则
,则 6分
6分
将上述两式相加得: 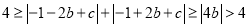 ,得
,得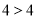 ,产生矛盾
,产生矛盾
∴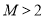 8分
8分
(3)【解析】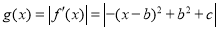
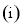 当
当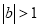 时,由
时,由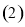 可知
可知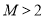 9分
9分
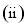 当
当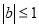 时,函数
时,函数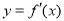 的对称轴
的对称轴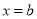 位于区间
位于区间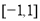 之内
之内
此时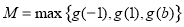 ,由
,由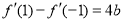 ,有
,有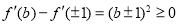
①若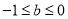 ,则
,则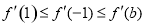 ,则
,则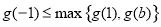
于是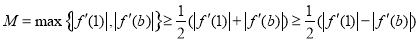
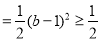 11分
11分
②若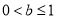 ,则
,则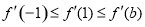 ,则
,则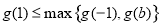 ,
,
于是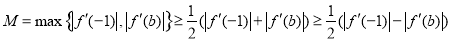
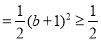 , 13分
, 13分
综上可知,对任意的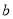 、
、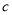 都有
都有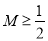
而当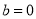 ,
,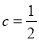 时,
时,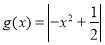 在区间
在区间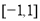 上的最大值
上的最大值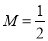
故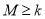 对任意的
对任意的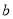 、
、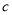 恒成立的
恒成立的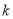 的最大值为
的最大值为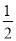 14分
14分
考点:考查了利用导数研究函数的极值,利用导数求函数在闭区间上的最值.

练习册系列答案
相关题目











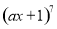 的展开式中,
的展开式中,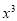 项的系数是
项的系数是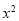 项系数和
项系数和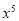 项系数的等比中项,则实数
项系数的等比中项,则实数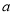 的值为
的值为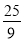 B.
B.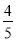 C.
C.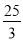 D.
D.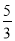
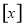 表示不超过
表示不超过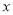 的最大整数,函数
的最大整数,函数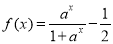
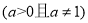 ,
,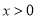 时恒有
时恒有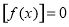 ,则实数
,则实数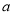 的取值范围是( )
的取值范围是( )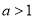 B.
B.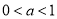 C.
C.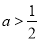 D.
D.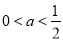
 ,
, ,
, ,
, ,
, 中任取两个不同字母,则取到字母
中任取两个不同字母,则取到字母 的概率为 .
的概率为 . B.
B. C.
C. D.
D.
 ,
,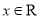 .
.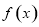 的最大值和最小正周期;
的最大值和最小正周期;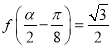 ,
,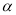 是第二象限角,求
是第二象限角,求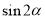 .
. 的解集是____________.
的解集是____________. 满足
满足 且
且 则向量
则向量 的夹角为__________.
的夹角为__________.