题目内容
一个均匀的正方体，把其中相对的面分别涂上红色、黄色、蓝色，随机向上抛出，正方体落地时“向上面为红色”的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：由随机抛正方体，有6种等可能的结果，正方体落地时“向上面为红色2种情况，直接利用概率公式求解即可求得答案．
解答：
解：∵由随机抛正方体，有6种等可能的结果，正方体落地时“向上面为红色2种情况，
∴正方体落地时“向上面为红色”的概率是
=
．
故选：B
∴正方体落地时“向上面为红色”的概率是
| 2 |
| 6 |
| 1 |
| 3 |
故选：B
点评：本题考查了概率公式的应用．注意概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
已知复数z=
，则（ ）
| 2 |
| -1+i |
| A、z的虚部为-1 |
| B、z的实部为1 |
| C、|z|=2 |
| D、z的共轭复数为1+i |
已知点P的极坐标是（2，
），则过点P且平行极轴的直线方程是（ ）
| π |
| 6 |
| A、ρ=1 | ||
| B、ρ=sinθ | ||
C、ρ=-
| ||
D、ρ=
|
下列函数中，最小正周期为π，且图象关于直线x=
成轴对称图形的（ ）
| π |
| 3 |
A、y=sin（2x-
| ||||
B、y=sin（2x+
| ||||
C、y=sin（2x-
| ||||
D、y=sin（
|
已知变量x与y之间一组对应数据如表格所示，经计算它们的回归直线方程为
=2.3x+0.8，定义ei=yi-
i为第i组数据的残差，如果要去除残差绝对值最大的那组数据，则应该去除（ ）
 |
| y |
|
| y |
| 序号i | 1 | 2 | 3 | 4 |
| xi | 0 | 1 | 2 | 3 |
| yi | 1 | 3 | 5 | 8 |
| A、第1组 | B、第2组 |
| C、第3组 | D、第4组 |
2014年索契冬季奥运会的花样滑冰项目上，8个评委为某选手打出的分数如茎叶图所示，则这些数据的中位数是（ ）| A、84 | B、85 |
| C、86 | D、87.5 |
已知点P（-1，1）与点Q（3，5）关于直线l对称，则直线l的方程为（ ）
| A、x-y+1=0 |
| B、x+y=0 |
| C、x+y-4=0 |
| D、x-y=0 |
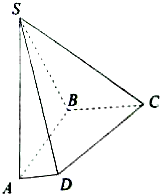如图所示，在四棱锥S-ABCD中，底面ABCD是直角梯形，SA⊥平面ABCD，且AD∥BC，AB⊥AD，BC=2AD=2，AB=AS=