题目内容
将下面的平面图形(每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四面体后,直线 与
与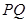 是异面直线的是( )
是异面直线的是( )
C
① ② ③ ④
| A.①② | B.②④ | C.①④ | D.①③ |
C
解析试题分析:第一个图中,直线 与
与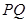 是相邻侧面的两条不相交,不平行的直线,故是异面直线。第二个图中,由于折叠后可知,MN与PQ是相交直线,故不是异面直线。第三个图中,由于利用平行的传递性,折叠前后平行性不变,第四个图中,根据异面直线的判定定理可知成立。故选C.
是相邻侧面的两条不相交,不平行的直线,故是异面直线。第二个图中,由于折叠后可知,MN与PQ是相交直线,故不是异面直线。第三个图中,由于利用平行的传递性,折叠前后平行性不变,第四个图中,根据异面直线的判定定理可知成立。故选C.
考点:本题主要考查了异面直线的概念的运用。
点评:解决该试题的关键是通过折叠图前后的关系,还原为几何体,然后分析两直线是否是不是共面直线的问题。

练习册系列答案
相关题目
四面体的五条棱长都是2,另一条棱长为1,则四面体的体积为( )。
A. | B. | C. | D. |
各棱长均为 的三棱锥的表面积为
的三棱锥的表面积为
A. | B. | C.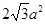 | D. |
对于一个底边在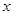 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的 ( )
轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的 ( )
| A. 2倍 | B. 倍 倍 | C. 倍 倍 | D. 倍 倍 |
如图,在正方体 中,
中, 为
为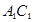 的中点,则异面直线
的中点,则异面直线 与
与 所成的角为( )
所成的角为( )
| A.30° | B.45° | C.60° | D.90 ° |
在正方体 中,
中, 是棱
是棱 的中点,则
的中点,则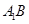 与
与 所成角的余弦值为( )
所成角的余弦值为( )
A.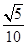 | B. | C. | D. |
正方体 ,棱长为
,棱长为 ,点
,点 到截面
到截面 的距离为( )
的距离为( )
A. | B.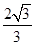 | C. | D. |
在三棱柱 中,各棱长相等,侧棱垂直于底面,点
中,各棱长相等,侧棱垂直于底面,点 是侧面
是侧面 的中心,则
的中心,则 与平面
与平面 所成角的大小是( )
所成角的大小是( )
A. | B. | C. | D. |

