如图.在正方体中.为的中点.则异面直线与所成的角为( )A．30° B．45° C．60° D．90 ° 题目和参考答案——青夏教育精英家教网—

题目内容

如图，在正方体中，为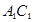的中点，则异面直线与所成的角为(　　)

A．30°

B．45°

C．60°

D．90 °

解析试题分析：因为底面ABCD为正方形，所以,又因为,
所以所以，所以异面直线CE与BD所成的角为.
考点：正方体的性质，异面直线所成的角.
点评：本小题实质是证明直线CE与BD垂直，所以可以利用线面垂直的性质定理只需证明即可.

练习册系列答案

相关题目

若一个球的表面积为4，则这个球的体积是（）

将边长为的正方形沿对角线折起，使得平面平面，在折起后形成的三棱锥中，给出下列三个命题：
①面是等边三角形； ②； ③三棱锥的体积是.
其中正确命题的个数为( )

将半径为R的圆面剪切去如图中的阴影部分，沿图所画的线折成一个正三棱锥，这个正三棱锥的侧面与底面所成的二面角的余弦值是（）

A．	B．
C．	D．

右图是某四棱锥的三视图，则该几何体的表面积等于 ( )

将下面的平面图形（每个点都是正三角形的顶点或边的中点）沿虚线折成一个正四面体后，直线与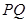是异面直线的是（）
C
① ② ③ ④

正方体的内切球的体积为, 则此正方体的表面积是

将正方形（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为（）.

A、 B、 C、 D、

侧棱长为2的正三棱锥，若其底面周长为9，则该正三棱锥的体积是

试题分类