题目内容
四面体的五条棱长都是2,另一条棱长为1,则四面体的体积为( )。
A. | B. | C. | D. |
C
解析试题分析:设四面体为A-BCD,其中AB=BC=CD=AC=2,AD=1,取AD的中点E,BC的中点F,连接CE、BE、EF,则AD⊥面BCE,BE=CE= ,EF=
,EF= ,所以
,所以 .
.
考点:三棱锥的体积公式。
点评:要求四面体的体积关键是求出四面体的高,做此题的关键是把四面体A-BCD的体积转化为三棱锥-BCE和三棱锥C-BCE的体积之和。此题为中档题。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
若一个球的表面积为4 ,则这个球的体积是( )
,则这个球的体积是( )
A. | B. | C. | D. |
将下面的平面图形(每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四面体后,直线 与
与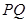 是异面直线的是( )
是异面直线的是( )
C
① ② ③ ④
| A.①② | B.②④ | C.①④ | D.①③ |




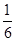
 的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是( )
的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是( )






 ,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )