题目内容
已知中心在原点,焦点在x轴上,离心率为
的椭圆过点(
,
).
(1)求椭圆方程;
(2)设不过原点O的直线l,与该椭圆交于P,Q两点,直线OP,PQ,OQ的斜率依次为k1、k、k2,满足k1、k、k2依次成等比数列,求△OPQ面积的取值范围.
| ||
| 2 |
| 2 |
| ||
| 2 |
(1)求椭圆方程;
(2)设不过原点O的直线l,与该椭圆交于P,Q两点,直线OP,PQ,OQ的斜率依次为k1、k、k2,满足k1、k、k2依次成等比数列,求△OPQ面积的取值范围.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:等差数列与等比数列,圆锥曲线的定义、性质与方程
分析:(1)设出椭圆的方程,将已知点代入椭圆的方程及利用椭圆的离心率公式得到关于椭圆的三个参数的等式,解方程组求出a,b,c的值,代入椭圆方程即可.
(2)设出直线的方程,将直线方程与椭圆方程联立,消去x得到关于y的二次方程,利用韦达定理得到关于两个交点的坐标的关系,将直线OP,PQ,OQ的斜率用坐标表示,据已知三个斜率成等比数列,列出方程,将韦达定理得到的等式代入,求出k的值,利用判别式大于0得到m的范围,将△OPQ面积用m表示,求出面积的范围.
(2)设出直线的方程,将直线方程与椭圆方程联立,消去x得到关于y的二次方程,利用韦达定理得到关于两个交点的坐标的关系,将直线OP,PQ,OQ的斜率用坐标表示,据已知三个斜率成等比数列,列出方程,将韦达定理得到的等式代入,求出k的值,利用判别式大于0得到m的范围,将△OPQ面积用m表示,求出面积的范围.
解答:
解:(1)由题意设椭圆方程为
+
=1(a>b>0),
由
,解得:a2=4,b2=1.
∴椭圆方程为
+y2=1;
(2)由题意设PQ所在直线方程为y=kx+m,
由
,得(1+4k2)x2+8kmx+4(m2-1)=0.
则△=64k2b2-16(1+4k2b2)(b2-1)=16(4k2-m2+1)>0,
且x1+x2=
,x1x2=
.
故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
∵直线OP,PQ,OQ的斜率依次成等比数列,
∴
•
=
=k2,
即
+m2=0,又m≠0,
∴k2=
,即k=±
.
由于直线OP,OQ的斜率存在,且△>0,得
0<m2<2且m2≠1.
设d为点O到直线l的距离,
则S△OPQ=
d|PQ|=
|x1-x2||m|=
.
∴S△OPQ的取值范围为(0,1).
| x2 |
| a2 |
| y2 |
| b2 |
由
|
∴椭圆方程为
| x2 |
| 4 |
(2)由题意设PQ所在直线方程为y=kx+m,
由
|
则△=64k2b2-16(1+4k2b2)(b2-1)=16(4k2-m2+1)>0,
且x1+x2=
| -8km |
| 1+4k2 |
| 4(m2-1) |
| 1+4k2 |
故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
∵直线OP,PQ,OQ的斜率依次成等比数列,
∴
| y1 |
| x1 |
| y2 |
| x2 |
| k2x1x2+km(x1+x2)+m2 |
| x1x2 |
即
| -8k2m2 |
| x1x2 |
∴k2=
| 1 |
| 4 |
| 1 |
| 2 |
由于直线OP,OQ的斜率存在,且△>0,得
0<m2<2且m2≠1.
设d为点O到直线l的距离,
则S△OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| m2(2-m2) |
∴S△OPQ的取值范围为(0,1).
点评:本题考查了椭圆方程的求法,考查了直线与圆锥曲线的位置关系,考查了等差数列的应用,训练了数学转化思想方法,着重考查了设而不求的解题思想方法,是压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
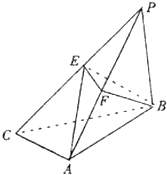 如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=BA=CA=4
如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=BA=CA=4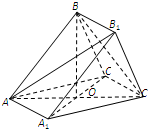 如图所示,三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面A1ACC1,
如图所示,三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面A1ACC1,