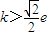题目内容
已知a>0,函数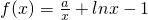 (其中e为自然对数的底数).
(其中e为自然对数的底数).
(Ⅰ)求函数f(x)在区间(0,e]上的最小值;
(Ⅱ)设数列{an}的通项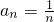 ,Sn是前n项和,证明:Sn-1<lnn(n≥2).
,Sn是前n项和,证明:Sn-1<lnn(n≥2).
(Ⅰ)解:求导函数,令其等于0,即 ,可得x=a
,可得x=a
若a≥e时,函数f(x)在区间(0,e]是减函数,∴ ;
;
0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,∴f(x)min=f(a)=lna;
(Ⅱ)证明:由(Ⅰ)可知,a=1时,函数f(x)在定义域的最小值为0,∴ 在[1,+∞)上成立
在[1,+∞)上成立
令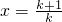 得
得 
令k=1,2,3,…,(n-1),可得 ,
, ,…,
,…,
∵数列{an}的通项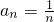 ,Sn是前n项和,∴叠加,可得Sn-1<lnn(n≥2)
,Sn是前n项和,∴叠加,可得Sn-1<lnn(n≥2)
分析:(Ⅰ)求导函数,令其等于0,可得x=a.若a≥e时,函数f(x)在区间(0,e]是减函数;0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,故可得函数f(x)在区间(0,e]上的最小值;
(Ⅱ)先证明 在[1,+∞)上成立,令
在[1,+∞)上成立,令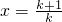 得
得  ,再令k=1,2,3,…,(n-1),叠加,即可得出结论.
,再令k=1,2,3,…,(n-1),叠加,即可得出结论.
点评:本题考查导数知识的运用,考查分类讨论的数学思想,考查不等式的证明,解题的关键是正确求导函数.
 ,可得x=a
,可得x=a若a≥e时,函数f(x)在区间(0,e]是减函数,∴
 ;
;0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,∴f(x)min=f(a)=lna;
(Ⅱ)证明:由(Ⅰ)可知,a=1时,函数f(x)在定义域的最小值为0,∴
 在[1,+∞)上成立
在[1,+∞)上成立令
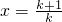 得
得 
令k=1,2,3,…,(n-1),可得
 ,
, ,…,
,…,
∵数列{an}的通项
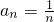 ,Sn是前n项和,∴叠加,可得Sn-1<lnn(n≥2)
,Sn是前n项和,∴叠加,可得Sn-1<lnn(n≥2)分析:(Ⅰ)求导函数,令其等于0,可得x=a.若a≥e时,函数f(x)在区间(0,e]是减函数;0<a<e时,函数f(x)在区间(0,a]是减函数,[a,e]是增函数,故可得函数f(x)在区间(0,e]上的最小值;
(Ⅱ)先证明
 在[1,+∞)上成立,令
在[1,+∞)上成立,令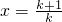 得
得  ,再令k=1,2,3,…,(n-1),叠加,即可得出结论.
,再令k=1,2,3,…,(n-1),叠加,即可得出结论.点评:本题考查导数知识的运用,考查分类讨论的数学思想,考查不等式的证明,解题的关键是正确求导函数.

练习册系列答案
相关题目
已知k>0,函数f(x)=kx2-lnx在其定义域上有两个零点,则实数k的取值范围是( )
A、k>
| ||||
B、0<k<
| ||||
C、k>
| ||||
D、0<k<
|