题目内容
15.已知函数f(x)=cos4x-2cossinx-sin4x+1(1)求f(x)的最小正周期和最大值;
(2)求f(x)的单调递增区间.
分析 (1)首先,根据二倍角公式,化简函数解析式得到f(x)=$\sqrt{2}$cos(2x+$\frac{π}{4}$)+1,然后确定其周期和最大值即可;
(2)直接结合余弦函数的单调区间进行求解即可.
解答 解:(1)∵函数f(x)=cos4x-2cossinx-sin4x+1
=(cos2x+sin2x(cos2x-sin2x)-2sinxcosx+1
=cos2x-sin2x-sin2x+1
=cos2x-sin2x+1
=$\sqrt{2}$cos(2x+$\frac{π}{4}$)+1
∴f(x)=$\sqrt{2}$cos(2x+$\frac{π}{4}$)+1
∴周期T=$\frac{2π}{2}$=π,
最大值为:1+$\sqrt{2}$.
(2)令-π+2kπ≤2x+$\frac{π}{4}$≤2kπ,k∈Z,
∴-$\frac{5π}{8}$+kπ≤x≤-$\frac{π}{8}$+kπ,
∴f(x)的单调递增区间[-$\frac{5π}{8}$+kπ,-$\frac{π}{8}$+kπ],(k∈Z).
点评 本题重点考查了二倍角公式、辅助角公式、三居函数的图象与性质等知识,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
3.已知z=$\frac{2-{i}^{3}}{1-i}$,i是虚数单位,则复数在复平面上对应点落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.函数f(x)=x2-|x-$\frac{1}{4}$|的零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
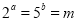 ,且
,且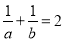 ,则
,则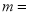 __________.
__________.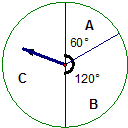 五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.