题目内容

7．函数f（x）=x2-|x-$\frac{1}{4}$|的零点的个数为（　　）
A．1B．2C．3D．4

分析 函数f（x）=x2-|x-$\frac{1}{4}$|的零点的个数，即函数y=x2，与y=|x-$\frac{1}{4}$|的图象的交点的个数，数列结合可得答案．

解答 解：函数f（x）=x2-|x-$\frac{1}{4}$|的零点的个数，
即函数y=x2与y=|x-$\frac{1}{4}$|的图象的交点的个数，
在同一坐标系中画出函数y=x2与y=|x-$\frac{1}{4}$|的图象如下图所示：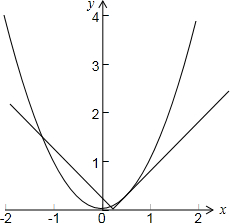

由图可得，两个函数图象共有3个交点，
故函数f（x）=x2-|x-$\frac{1}{4}$|的零点的个数为3个，
故选：C

点评 本题考查的知识点是函数零点的判定定理，难度不大，属于基础题．

练习册系列答案
相关题目
19．位加强食品安全监督，某市质量检查部门对某食品加工厂进行了抽样调查，抽到的产品一共有162件，并从001～162对它们进行编号，根据食品的编号，再用系统抽样的方法在其中抽取一个容量为9的样本，已知022号在样本中，那么样体中最大的编号是 （　　）
A．147B．150C．148D．149

设，则下列关系中正确的是（ ）

A． B．

C． D．
15．已知函数f（x）=cos4x-2cossinx-sin4x+1
（1）求f（x）的最小正周期和最大值；
（2）求f（x）的单调递增区间．
2．设函数f（x）=ln（1+x），g（x）=xf′（x）（x≥0），其中f′（x）是f（x）的导函数．
（1）若a≤1，求证：f（x）≥ag（x）．
（2）若g1（x）=g（x），gn+1（x）=g（gn（x）），n∈N+，求g1（x），g2（x），g3（x）解析式，猜想gn（x）的解析式，并用数学归纳法证明．
12．不等式$\frac{x-1}{6-x}$＜0的解集是{x|x＞6或x＜1}．
19．当无理数x=3$±\sqrt{2}$-1时，代数式$\frac{{x}^{2}-2x+4}{{x}^{2}-3x+3}$的值是整数．
16．已知数列{an}各项均不为0，其前n项和为Sn，且对任意n∈N*都有（1-p）Sn=p-pan（p为大于1的常数），记f（n）=$\frac{{1+C_n^1{a_1}+C_n^2{a_2}+…+C_n^n{a_n}}}{{{2^n}{S_n}}}$．
（1）求an；
（2）求证：f（1）+f（2）+…+f（2n-1）≥（2n-1）f（n），（n∈N*）．
17．若函数f（x）=$\left\{\begin{array}{l}{\frac{1}{x}，x＜0}\\{（\frac{1}{3}）^{x}，x≥0}\end{array}\right.$ 则f（f（-2））=-2，不等式|f（x）|≥$\frac{1}{3}$的解集为[-3，1]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网