题目内容
如图，在△ABC中，AD为三角形BC边上的中线，且AE=2EC，BE交AD于G，求
，及
的值．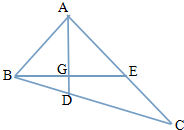
| AG |
| GD |
| BG |
| GE |
考点：三角形中的几何计算
专题：解三角形
分析：作DF∥AC，交BE于点F；作EM∥AD，M∈BC，根据线段长度间的关系以及平行线的性质，求得
，及
的值．
| AG |
| GD |
| BG |
| GE |
解答：
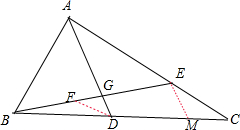解：作DF∥AC，交BE于点F，∵D为BC的中点，∴DF为△BCE的中位线，
∴DF∥EC，DF=
EC．
由AE=2EC，可得DF=
AE．
再根据平行线的性质，可得
=
=4．
作EM∥AD，M∈BC，根据AE=2EC，可得CM=
DC．
再根据平行线的性质，可得
=
=
=
．
解：作DF∥AC，交BE于点F，∵D为BC的中点，∴DF为△BCE的中位线，∴DF∥EC，DF=
| 1 |
| 2 |
由AE=2EC，可得DF=
| 1 |
| 4 |
再根据平行线的性质，可得
| AG |
| GD |
| AE |
| DF |
作EM∥AD，M∈BC，根据AE=2EC，可得CM=
| 1 |
| 3 |
再根据平行线的性质，可得
| BG |
| GE |
| BD |
| DM |
| DC | ||
DC-
|
| 3 |
| 2 |
点评：本题主要考查平行线的性质，作出辅助线DF∥EC、EM∥AD，是解题的关键，属于中档题．
练习册系列答案
相关题目
已知（x2-
）5的展开式中的常数项为T，f（x）是以T为周期的偶函数，且当x∈[0，1]时，f（x）=x，若在区间[-1，3]内，函数g（x）=f（x）-kx-2k有4个零点，则实数k的取值范围是（ ）
| 1 | ||
|
A、（0，
| ||
B、[0，
| ||
C、（0，
| ||
D、[0，
|
某几何体的三视图如图所示，若其正视图为等腰梯形，侧视图为正三角形，则该几何体的表面积为（ ）A、2
| ||
| B、6 | ||
C、4
| ||
| D、8 |