题目内容
已知函数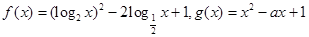
(1)求函数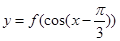 的定义域;
的定义域;
(2)若存在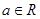 ,对任意
,对任意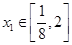 ,总存在唯一
,总存在唯一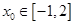 ,使得
,使得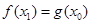 成立.求实数
成立.求实数 的取值范围.
的取值范围.
(1)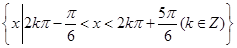
(2)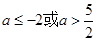
解析试题分析:解:(1)由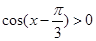 解得
解得
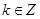
即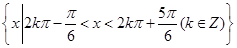
(2)首先,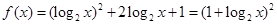
∵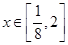 ∴
∴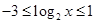 ∴函数
∴函数 的值域为
的值域为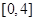
其次,由题意知: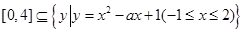 ,且对任意
,且对任意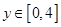 ,总存在唯一
,总存在唯一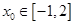 ,使得
,使得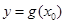 .以下分三种情况讨论:
.以下分三种情况讨论:
①当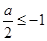 时,则
时,则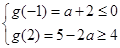 ,解得
,解得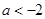 ;
;
②当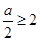 时,则
时,则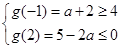 ,解得
,解得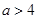 ;
;
③当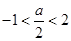 时,则
时,则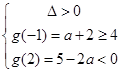 或
或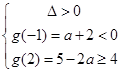 ,解得
,解得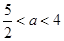 ;
;
综上: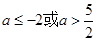
考点:三角函数的性质
点评:主要是考查了三角函数的性质和对数函数的不等式的求解,以及二次方程根的分布问题,属于中档题。

练习册系列答案
相关题目
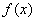 与时间
与时间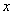 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: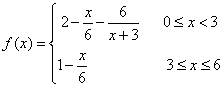 ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于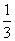 时,才能对污
时,才能对污 ,求
,求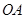 ,
,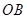 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段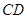 和曲线段
和曲线段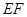 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥 分别修建与
分别修建与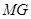 、
、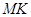 ,且以
,且以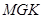 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段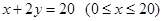 ,曲线段
,曲线段 ,设点
,设点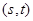 ,记
,记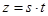 .(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)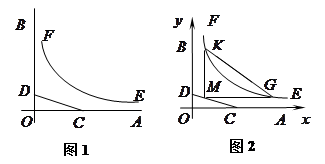
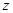 的取值范围;
的取值范围;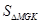 关于
关于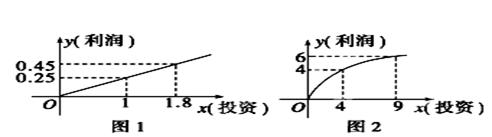
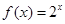 ,
,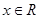 .
.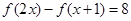 ;
;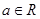 ,求函数
,求函数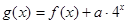 在区间
在区间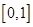 上的最大值
上的最大值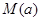 的表达式;
的表达式;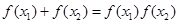 ,
,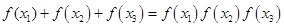 ,求
,求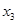 的最大值.
的最大值.
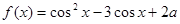 的最大值为6.求
的最大值为6.求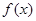 最小值.
最小值.