题目内容
已知函数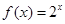 ,
,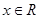 .
.
(Ⅰ)解方程: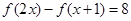 ;
;
(Ⅱ)设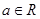 ,求函数
,求函数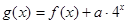 在区间
在区间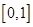 上的最大值
上的最大值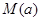 的表达式;
的表达式;
(Ⅲ)若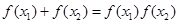 ,
,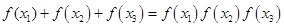 ,求
,求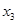 的最大值.
的最大值.
(Ⅰ)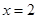 .(Ⅱ)
.(Ⅱ)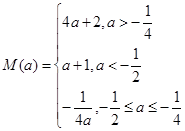 .(Ⅲ)
.(Ⅲ)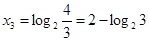 .
.
解析试题分析:(Ⅰ)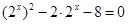 ,
,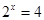 或
或 (舍去),
(舍去),
所以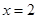 .
.
(Ⅱ)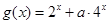 ,
,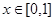 ,
,
令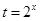 ,则
,则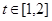 ,
,
①当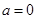 时,
时,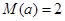 ,
,
②当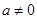 时,
时, ,
,
若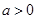 ,则
,则 ,
,
若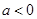 ,当
,当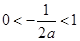 ,即
,即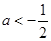 时,
时,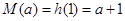 ,
,
当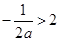 ,即
,即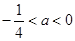 时,
时,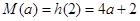 ,
,
当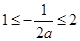 ,即
,即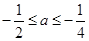 时,
时,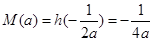 ,
,
综上,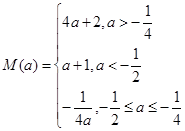 .
.
(Ⅲ)由题意知: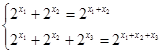
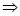
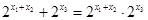 ,
,
所以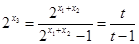 ,
,
其中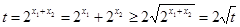 ,所以
,所以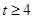 ,
,
由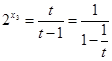 知
知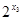 的最大值是
的最大值是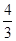 ,又
,又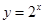 单调递增,
单调递增,
所以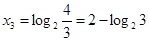 .
.
考点:本题主要考查分段函数的概念,指数函数的性质,二次函数的图象和性质,均值定理的应用。
点评:中档题,本题综合考查分段函数的概念,指数函数的性质,二次函数的图象和性质,均值定理的应用。利用换元思想,将问题转化成二次函数问题,通过变换函数表达式,创建应用均值定理的条件,体现应用数学知识的灵活性。

练习册系列答案
相关题目
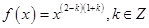 ,且
,且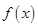 在
在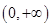 上单调递增.
上单调递增.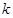 的值,并写出相应的函数
的值,并写出相应的函数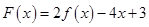 在区间
在区间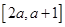 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;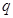 ,使函数
,使函数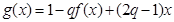 在区间
在区间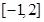 上的值域为
上的值域为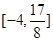 若存在,求出
若存在,求出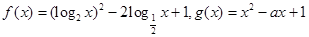
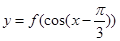 的定义域;
的定义域;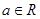 ,对任意
,对任意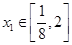 ,总存在唯一
,总存在唯一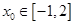 ,使得
,使得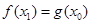 成立.求实数
成立.求实数 的取值范围.
的取值范围. 的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后
的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后 到达现场开始救火,已知消防队在现场每人每分钟平均可灭火
到达现场开始救火,已知消防队在现场每人每分钟平均可灭火 ,所消耗的灭火材料、劳务津贴等费用每人每分钟
,所消耗的灭火材料、劳务津贴等费用每人每分钟 元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人
元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人 元,而每烧毁
元,而每烧毁 森林的损失费为
森林的损失费为 元,设消防队派了
元,设消防队派了 名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时
名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时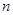
 .
.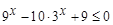 ,求函数
,求函数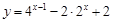 的最大值和最小值;
的最大值和最小值; 在
在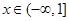 上f (x)
上f (x)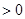 恒成立,求a的取值范围.
恒成立,求a的取值范围.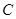 (单位:万元)与日产量
(单位:万元)与日产量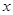 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式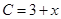 ,每日的销售额
,每日的销售额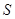 (单位:万元)与日产量
(单位:万元)与日产量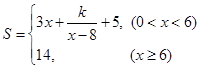
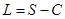 ,且当
,且当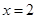 时,
时,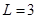 .
.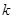 的值;
的值;
 元(
元( 元.(14分)
元.(14分)