题目内容
12.设a为实数,函数f(x)=x3-x2-x+a(1)求f(x)的极值
(2)曲线y=f(x)与x轴仅有一个交点,求a的取值范围.
分析 (1)函数连续可导,只需讨论满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值点,求出极值.
(2)曲线f(x)与x轴仅有一个交点,可转化成f(x)极大值<0或f(x)极小值>0即可.
解答 解:(1)令f'(x)=3x2-2x-1=0得:x1=-$\frac{1}{3}$,x2=1.
又∵当x∈(-∞,-$\frac{1}{3}$)时,f'(x)>0;
当x∈(-$\frac{1}{3}$,1)时,f'(x)<0;
当x∈(1,+∞)时,f'(x)>0;
∴x1=-$\frac{1}{3}$与x2=1分别为f(x)的极大值与极小值点.
∴f(x)极大值=f(-$\frac{1}{3}$)=a+$\frac{5}{27}$;f(x)极小值=a-1;
(2)∵f(x)在(-∞,-$\frac{1}{3}$)上单调递增,
∴当x→-∞时,f(x)→-∞;
又f(x)在(1,+∞)单调递增,当x→+∞时,f(x)→+∞
∴当f(x)极大值<0或f(x)极小值>0时,曲线f(x)与x轴仅有一个交点.
即a+$\frac{5}{27}$<0或a-1>0,
∴a∈(-∞,-$\frac{5}{27}$)∪(1,+∞).
点评 本题主要考查了利用导数研究函数的极值,以及函数的单调性,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
4.若集合A={x|y=(x-1)0},B={y|y=x2,x∈R},则A∩B等于( )
| A. | {x|-1≤x≤1} | B. | {x|x≥0} | C. | {x|x≥0且x≠1} | D. | ∅ |
1.运行如图所示的程序框图,若输出的点恰有3次落在直线上y=x,则判断框中可填写的条件是( )
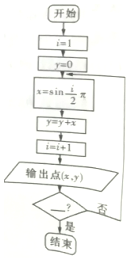

| A. | i>8 | B. | i>7 | C. | i>6 | D. | i>5 |
2.已知集合A={x|ax2+x-3=0},B={x|3≤x<7},若A∩B≠∅,则实数a的取值集合为( )
| A. | [-$\frac{1}{12}$,0] | B. | [-$\frac{1}{12}$,-$\frac{4}{49}$) | C. | (-$\frac{4}{49}$,0] | D. | [-$\frac{4}{49}$,0] |