题目内容
如图,等腰梯形 中,
中, 且
且 ,
, . 以
. 以 ,
, 为焦点,且过点
为焦点,且过点 的双曲线的离心率为
的双曲线的离心率为 ;以
;以 ,
, 为焦点,且过点
为焦点,且过点 的椭圆的离心率为
的椭圆的离心率为 ,则
,则 的取值范围为( )
的取值范围为( )

 中,
中, 且
且 ,
, . 以
. 以 ,
, 为焦点,且过点
为焦点,且过点 的双曲线的离心率为
的双曲线的离心率为 ;以
;以 ,
, 为焦点,且过点
为焦点,且过点 的椭圆的离心率为
的椭圆的离心率为 ,则
,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
B
试题分析:如下图所示,分别过点
 、
、 作
作 ,
, ,垂足分别为点
,垂足分别为点 、
、 ,连接
,连接 ,
,
易知
 ,
, ,且
,且 ,
, ,由勾股定理得
,由勾股定理得 ,
, ,由勾股定理得
,由勾股定理得 ,
, ,设以
,设以 ,
, 为焦点,且过点
为焦点,且过点 的双曲线的实轴长为
的双曲线的实轴长为 ,焦距为
,焦距为 ,以
,以 ,
, 为焦点,且过点
为焦点,且过点 的椭圆的长轴长为
的椭圆的长轴长为 ,焦距为
,焦距为 ,则
,则 ,
, ,根据双曲线的定义知
,根据双曲线的定义知 ,
, ,根据椭圆的定义知
,根据椭圆的定义知 ,
, ,
,
 ,
,
 ,
, ,而
,而 在
在 上单调递增,
上单调递增, ,令
,令
 ,则函数
,则函数 在
在 上单调递减,则当
上单调递减,则当 时,
时,
 ,即
,即 的取值范围是
的取值范围是 .
.
练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
 的两个焦点
的两个焦点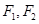 和上下两个顶点
和上下两个顶点 是一个边长为2且∠F1B1F2为
是一个边长为2且∠F1B1F2为 的菱形的四个顶点.
的菱形的四个顶点. 的方程;
的方程; (
( )的直线
)的直线 与椭圆
与椭圆 两点,A为椭圆的右顶点,直线
两点,A为椭圆的右顶点,直线 、
、 分别交直线
分别交直线 于点
于点 、
、 ,线段
,线段 的中点为
的中点为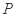 ,记直线
,记直线 的斜率为
的斜率为 .求证:
.求证: 为定值.
为定值. 的长轴两端点分别为
的长轴两端点分别为 ,
, 是椭圆上的动点,以
是椭圆上的动点,以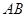 为一边在
为一边在 轴下方作矩形
轴下方作矩形 ,使
,使 ,
, 交
交 ,
, 交
交 .
.
 ,且
,且 为椭圆上顶点时,
为椭圆上顶点时, 的面积为12,点
的面积为12,点 到直线
到直线 ,求椭圆的方程;
,求椭圆的方程; ,试证明:
,试证明: 成等比数列.
成等比数列.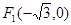 和
和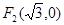 ,且椭圆过点
,且椭圆过点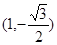 .
.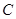 的方程;
的方程;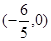 作不与
作不与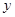 轴垂直的直线
轴垂直的直线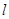 交该椭圆于
交该椭圆于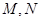 两点,
两点,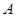 为椭圆的左顶点,试判断
为椭圆的左顶点,试判断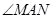 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.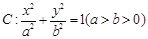 的离心率为
的离心率为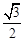 ,且经过点
,且经过点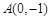 .
.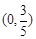 的直线与椭圆交于
的直线与椭圆交于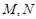 两点(
两点(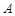 点不重合),
点不重合),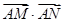 的值;
的值;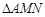 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线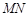 的方程.
的方程.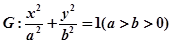 的离心率为
的离心率为 ,
,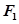 ,
, 为椭圆
为椭圆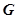 的两个焦点,点
的两个焦点,点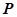 在椭圆
在椭圆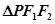 的周长为
的周长为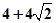 。
。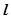 与椭圆
与椭圆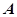 、
、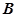 两点,若
两点,若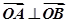 (
(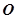 为坐标原点),求证:直线
为坐标原点),求证:直线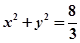 相切.
相切. 的圆心为
的圆心为 ,动圆
,动圆 过点
过点 ,且和圆
,且和圆 .
. 为曲线
为曲线 与曲线
与曲线
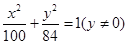


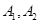 为椭圆
为椭圆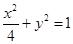 的左右顶点,在长轴
的左右顶点,在长轴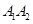 上随机任取点
上随机任取点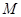 ,过
,过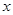 轴的直线交椭圆于点
轴的直线交椭圆于点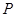 ,则使
,则使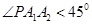 的概率为
的概率为


