题目内容
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结果相互独立,第1局甲当裁判.
,各局比赛的结果相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)X表示前4局中乙当裁判的次数,求X的数学期望.
解:(1)记A1表示事件“第2局结果为甲胜”,
A2表示事件“第3局甲参加比赛时,结果为甲负”,
A表示事件“第4局甲当裁判”,
则A=A1·A2.
P(A)=P(A1·A2)=P(A1)·P(A2)=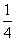 .
.
(2)X的可能取值为0,1,2.
记A3表示事件“第3局乙和丙比赛时,结果为乙胜”,
B1表示事件“第1局结果为乙胜丙”,
B2表示事件“第2局乙和甲比赛时,结果为乙胜”,
B3表示事件“第3局乙参加比赛时,结果为乙负”.
则P(X=0)=P(B1·B2·A3)=P(B1)P(B2)P(A3)=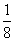 ,
,
P(X=2)=P(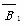 ·B3)=P(
·B3)=P(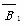 )P(B3)=
)P(B3)=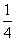 ,
,
P(X=1)=1-P(X=0)-P(X=2)=1-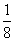 -
-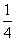 =
=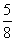 .
.
E(X)=0·P(X=0)+1·P(X=1)+2·P(X=2)=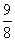 .
.

每一个父母都希望自己的孩子能升上比较理想的中学,于是就催生了“择校热”,这样“择校”的结果就导致了学生在路上耽误的时间增加了.若某生由于种种原因,每天只能6∶15骑车从家出发到学校,途径5个路口,这5个路口将家到学校分成了6个路段,每个路段的骑车时间是10分钟(通过路口的时间忽略不计),假定他在每个路口遇见红灯的概率均为 ,且该生只在遇到红灯或到达学校才停车.对每个路口遇见红灯的情况统计如下:
,且该生只在遇到红灯或到达学校才停车.对每个路口遇见红灯的情况统计如下:
| 红灯 | 1 | 2 | 3 | 4 | 5 |
| 等待时间(秒) | 60 | 60 | 90 | 30 | 90 |
(1)设学校规定7∶20后(含7∶20)到校即为迟到,求这名学生迟到的概率;
(2)设ξ表示该学生第一次停车时已经通过的路口数,求它的分布列.
由y=f(x)的图象向左平移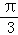 个单位,再把所得图象上所有点的横坐标伸长到原来的2倍得到y=2sin
个单位,再把所得图象上所有点的横坐标伸长到原来的2倍得到y=2sin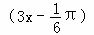 的图象,则 f(x)为( )
的图象,则 f(x)为( )
|
| A. | 2sin | B. | 2sin | C. | 2sin | D. | 2sin |

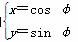 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=2cos
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=2cos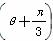 .
. B.
B.
 D.
D.

 B.
B.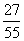 C.
C.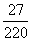 D.
D.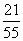
 满足
满足 ,则
,则 的取值范围是
的取值范围是 


