Question

已知圆C₁的参数方程为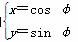 (φ为参数)，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C₂的极坐标方程为ρ＝2cos.

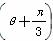(1)将圆C₁的参数方程化为普通方程，将圆C₂的极坐标方程化为直角坐标方程；

(2)圆C₁、C₂是否相交，若相交，请求出公共弦的长；若不相交，请说明理由．

Answer 1

解：(1)由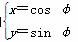得x²＋y²＝1，

由题意可知：ρ＝2cos＝cos θ－sin θ，

∴ρ²＝ρcos θ－ρsin θ

∴x²＋y²－x＋y＝0，即＝1

(2)圆心距d＝＝1<2，得两圆相交

由得A(1,0)，B，

∴|AB|＝＝.