题目内容
8.货车欲以x km/h的速度行驶去130km远的某地,按交通法规,限制x的允许范围是[50,100],假设汽油的价格为2元/升,而汽车耗油的速率是(2+$\frac{{x}^{2}}{360}$) 升/小时.司机的工资是14元/小时,试问最经济的车速是18$\sqrt{10}$km/h.这次行车的总费用最低是26$\sqrt{10}$元.分析 易知行驶时间t=$\frac{130}{x}$,x∈[50,100],从而可得y=[14+2(2+$\frac{{x}^{2}}{360}$)]$\frac{130}{x}$=130($\frac{18}{x}$+$\frac{x}{180}$),从而利用基本不等式求解最值.
解答 解:由题意知,行驶时间t=$\frac{130}{x}$,x∈[50,100],
记总费用为y元,
则y=[14+2(2+$\frac{{x}^{2}}{360}$)]$\frac{130}{x}$
=130($\frac{18}{x}$+$\frac{x}{180}$)
≥130×2×$\frac{\sqrt{10}}{10}$=26$\sqrt{10}$,
(当且仅当$\frac{18}{x}$=$\frac{x}{180}$,即x=18$\sqrt{10}$时,等号成立),
故答案为:18$\sqrt{10}$,26$\sqrt{10}$.
点评 本题考查了基本不等式在求解最值问题中的应用.

练习册系列答案
相关题目
16.已知等比数列{an}的公比为4,且a1+a2=20,设bn=log2an,则b2+b4+b6+…+b2n等于( )
| A. | n2+n | B. | 2n2+n | C. | 2(n2+n) | D. | 4(n2+n) |
13.某几何体的三视图如图所示,则该几何体的体积是( )
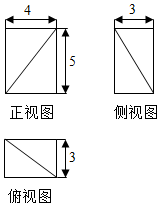

| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
20.从5名学生中选2名学生参加周日社会实验活动,学生甲被选中而学生乙没有被选中的方法种数是( )
| A. | 10 | B. | 6 | C. | 4 | D. | 3 |