题目内容
在△ABC中,角A、B、C所对的边分别是a、b、c,并且a2、b2、c2成等差数列,则角B的取值范围是 .
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:由等差数列的定义和性质可得2b2=a2 +c2 ,再由余弦定理可得cosB=
,利用基本不等式可得cosB≥
,从而求得角B的取值范围.
| a2+c2 |
| 4ac |
| 1 |
| 2 |
解答:
解:由题意可得2b2=a2 +c2 ,由余弦定理可得cosB=
=
≥
,
当且仅当a=c时,等号成立.
又 0<B<π,∴0<B≤
,
故答案为:0<B≤
.
| a2+c2-b2 |
| 2ac |
| a2+c2 |
| 4ac |
| 1 |
| 2 |
当且仅当a=c时,等号成立.
又 0<B<π,∴0<B≤
| π |
| 3 |
故答案为:0<B≤
| π |
| 3 |
点评:本题主要考查余弦定理、等差数列的定义和性质,以及基本不等式的应用,求得cosB≥
,是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目

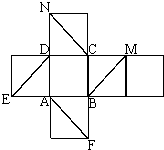 如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是
如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是