题目内容
4．已知P是非等边△ABC外接圆上任意一点，求：当P分别位于何处时，PA2+PB2+PC2分别取到最大值和最小值．分析 设外接圆半径为R，点O是外心，可得PA2+PB2+PC2=（$\overrightarrow{PO}$+$\overrightarrow{OA}$）2+（$\overrightarrow{PO}$+$\overrightarrow{OB}$）2+（$\overrightarrow{PO}$+$\overrightarrow{OC}$）2，由向量的运算和三角形的垂心的性质可得．
解答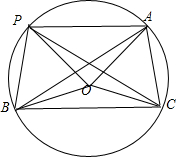 
解：如图，设非等边△ABC外接圆半径为R，点O是外心，
则PA2+PB2+PC2=（$\overrightarrow{PO}$+$\overrightarrow{OA}$）2+（$\overrightarrow{PO}$+$\overrightarrow{OB}$）2+（$\overrightarrow{PO}$+$\overrightarrow{OC}$）2
=6R2+2（$\overrightarrow{PO}$•$\overrightarrow{OA}$+$\overrightarrow{PO}$•$\overrightarrow{OB}$+$\overrightarrow{PO}$•$\overrightarrow{OC}$）
=6R2+2$\overrightarrow{PO}$•（$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$）
=6R2+2$\overrightarrow{PO}$•$\overrightarrow{OH}$ （H为△ABC垂心），
∴当P为OH的反向延长线与外接圆交点时，已知式子有最大值6R2+2R•OH；
当P为OH的延长线与外接圆交点时，已知式子有最小值6R2-2R•OH．
点评 本题考查三角形的外接圆的性质，涉及外心和垂心的性质以及向量的运算，属中档题．
