题目内容
9.已知点A(1,-2),B(4,0),P(a,1),N(a+1,1),当四边形PABN的周长最小时,则a的值为$\frac{5}{2}$.分析 由两点间距离公式得到欲求当四边形PABN的周长最小时a的值,只需求出$\sqrt{(a-1)^{2}+(1+2)^{2}}$+$\sqrt{(a-3)^{2}+(1-0)^{2}}$的最小值时的a值,只需x轴上的点(a,0)与(1,3)和(3,1)距离之和最小即可,由此能求出a的值.
解答 解:∵点A(1,-2),B(4,0),P(a,1),N(a+1,1),
∴四边形PABN的周长为
C=|PA|+|AB|+|BN|+|NP|
=$\sqrt{(a-1)^{2}+(1+2)^{2}}$+$\sqrt{(4-1)^{2}+(0+2)^{2}}$+$\sqrt{(a-3)^{2}+(1-0)^{2}}$+1
=$\sqrt{(a-1)^{2}+(1+2)^{2}}$+$\sqrt{(a-3)^{2}+(1-0)^{2}}$+$\sqrt{13}$+1,
∴欲求当四边形PABN的周长最小时a的值,
只需求出$\sqrt{(a-1)^{2}+(1+2)^{2}}$+$\sqrt{(a-3)^{2}+(1-0)^{2}}$的最小值时的a值.
由于$\sqrt{(a-1)^{2}+(1+2)^{2}}$+$\sqrt{(a-3)^{2}+(1-0)^{2}}$=$\sqrt{(a-1)^{2}+(0-3)^{2}}$+$\sqrt{(a-3)^{2}+(0-1)^{2}}$,
表示x轴上的点(a,0)与(1,3)和(3,1)距离之和,只需该距离之和最小即可.
利用对称的思想,可得该距离之和的最小值为(1,-3)与(3,1)间的距离,
且取得最小的a值为E(1,-3)与F(3,1)确定的直线与x轴交点的横坐标,
∵直线EF的斜率k=$\frac{1+3}{3-1}$=2,∴直线EF方程为y+3=2(x-1),化简得y=2x-5,
令y=0,得x=$\frac{5}{2}$,∴此时a的值为$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查实数值的求法,是中档题,解题时要认真审题,注意两点间距离公式和等价转化思想的合理运用.

| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c |
| A. | ±$\frac{5}{4}$ | B. | ±$\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | -$\frac{{\sqrt{5}}}{2}$ |
| A. | p∧q为真命题 | B. | (¬p)∧(¬q)为真命题 | C. | ¬(p∨q)为假命题 | D. | (¬p)∨q为假命题 |
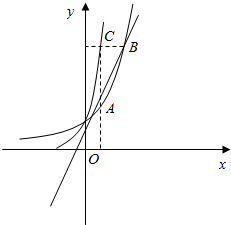 如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).
如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).