题目内容
12．若钝角△ABC的面积为10$\sqrt{3}$，且AB=5，AC=8，则BC等于$\sqrt{129}$．分析 利用三角形的面积公式求出A，再利用余弦定理求出BC．
解答 解：因为钝角△ABC的面积为10$\sqrt{3}$，且AB=5，AC=8，
所以$\frac{1}{2}$×5×8×sinA=10$\sqrt{3}$，
所以sinA=$\frac{\sqrt{3}}{2}$，
所以A=120°，
所以cosA=-$\frac{1}{2}$，
由余弦定理可得：BC=$\sqrt{{5}^{2}+{8}^{2}+2×5×8×\frac{1}{2}}$=$\sqrt{129}$．
故答案为：$\sqrt{129}$．
点评 本题考查三角形的面积公式，考查余弦定理的运用，比较基础．
练习册系列答案
备战中考寒假系列答案
相关题目
2．已知A={-2，2010，x2-1}，B={0，2010，x2-3x}，且A=B，则x的值为（ ）
| A． | 1 | B． | 0 | C． | -1 | D． | -1，1 |
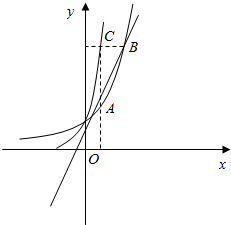如图，在平面直角坐标系xOy中，过原点O的直线与函数y=3x的图象交于A，B两点，过B作y轴的垂线交函数y=9x的图象于点C，若AC平行于y轴，则点A的坐标是（log32，2）．