题目内容
6．函数f（x）=asin（πx+α）+bcos（πx+β）+1008（a，b，α，β均为非零实数），若f（2016）=16，则f（2017）=2000．分析 由条件利用诱导公式求得 asinα+bcosβ=-992，从而求得f （2017）的值．
解答 解：∵f（x）=asin（πx+α）+bcos（πx+β）+1008，其中a，b，α，β均为非零实数，
若f（2016）=asin（2016π+α）+bcos（2016π+β）+1008=asinα+bcosβ+1008=16，
∴asinα+bcosβ=-992，
则 f （2017）=asin（2017π+α）+bcos（2017π+β）+1008=-asinα-bcosβ+1008=2000．
故答案为：2000．
点评 本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
相关题目
7．已知△ABC满足∠BAC=60°，BC=2，对于△ABC外接圆上一点D，满足∠BCD=45°，则BD=（ ）
| A． | $\sqrt{6}$ | B． | $\sqrt{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\frac{2\sqrt{6}}{3}$ |
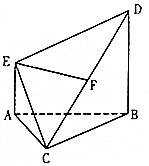如图，AE⊥平面ABC，AE∥BD，AB=BC=CA=BD=2AE=2，F为CD中点．
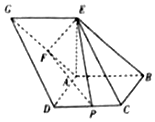如图，已知四边形ABCD和ABEG均为平行四边形，点E在平面ABCD内的射影恰好为点A，以BD为直径的圆经过点A，C，AG的中点为F，CD的中点为P，且AD=AB=AE
11．“直线ax+3y+3=0和直线4x+（a+1）y+4=0平行”的充要条件是“a=（ ）”
| A． | -4或3 | B． | -$\frac{3}{7}$ | C． | -3 | D． | -4 |