题目内容
某班5名学生负责校内3个不同地段的卫生工作，每个地段至少有1名学生的分配方案共有（ ）
| A、60种 | B、90种 |
| C、150种 | D、240种 |
考点：计数原理的应用
专题：排列组合
分析：根据题意，分2步进行分析：①、先将5名学生分成3组，每组至少一人，分析可得有2，2，1或3，1，1两种情况；分别求出每种情况的分组方法数目，再由分类计数原理可得全部的分组方法数目，②、将分好的3组对应3个公司，有A33=6种情况，进而由分步计数原理计算可得答案．
解答：
解：分2步进行分析：
①、先将5名学生分成3组，每组至少一人，有2，2，1或3，1，1两种情况；
若分成2，2，1的三组，有
=15种分组方法，
若分成3，1，1的三组，有
=10种分组方法，
则将5名学生分成3组，每组至少一人，有15+10=25种分组方法，
②、将分好的3组对应3个公司，有A33=6种情况，
故共有25×6=150种不同的分配方案．
故选：C
①、先将5名学生分成3组，每组至少一人，有2，2，1或3，1，1两种情况；
若分成2，2，1的三组，有
| ||||
|
若分成3，1，1的三组，有
| C | 3 5 |
则将5名学生分成3组，每组至少一人，有15+10=25种分组方法，
②、将分好的3组对应3个公司，有A33=6种情况，
故共有25×6=150种不同的分配方案．
故选：C
点评：本题考查分步、分类计数原理的运用，分析本题要先分组，再对应三个公司进行全排列，解题时注意排列、组合公式的灵活运用．
练习册系列答案
相关题目
不等式4x+log3x+x2＞5的解集为（ ）
| A、R |
| B、R+ |
| C、{x|x＞1} |
| D、{x|x＞2} |
在下列给出的函数：（1）y=
；（2）y=
；（3）y=x2+x中，幂函数的个数为（ ）
| x |
| 1 |
| x2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
已知幂函数f（x）=（m-3）xm，则下列关于f（x）的说法不正确的是（ ）
| A、f（x）的图象过原点 |
| B、f（x）的图象关于原点对称 |
| C、f（x）的图象关于y轴对称 |
| D、f（x）=x4 |
cos390°=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
集合A={x|2＜x＜7}，B={x|3≤x＜10}，A∩B=（ ）
| A、（2，10） |
| B、[3，7） |
| C、（2，3] |
| D、（7，10） |
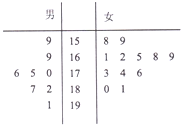第117届中国进出口商品交易会（简称2015年春季交广会）将于2015年4月15日在广州市举行，为了搞好接待工作，组委会在广州某大学分别招募8名男志愿者和12名女志愿者，现将这20名志愿者的身高组成如下茎叶图（单位：m），若身高在175cm以上（包括175cm）定义为“高个子”，身高在175cm以下（不包括175cm）定义为“非高个子”．