题目内容
已知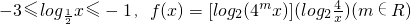 .
.
(1)求函数f(x)的最大值g(m)的解析式;
(2)若g(m)≥t+m+2对任意m∈[-4,0]恒成立,求实数t的取值范围.
解:(1)∵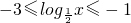 ,∴1≤log2x≤3,
,∴1≤log2x≤3,
∵f(x)=(2m+log2x)(2-log2x),令log2x=y∈[1,3],
∴f(x)=(2m+y)(2-t)=-[y-(1-m)]2+m2+2m+1,…(4分)
讨论对称轴 y=1-m,得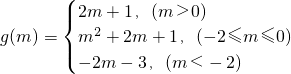 .…(10分)
.…(10分)
(2)根据题意:t≤g(m)-m-2对任意的m∈[-4,0]恒成立,
①当m∈[-4,-2)时,t≤-3m-5,由于-3m-5关于m单调递减,∴t≤-3(-2)-5=1.…(12分)
②当m∈[-2,0]时,t≤m2+m-1,
而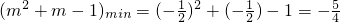 ,∴
,∴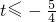 .…(15分)
.…(15分)
综上,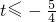 .…(16分)
.…(16分)
分析:(1)令log2x=y∈[1,3],可得f(x)=(2m+y)(2-t)=-[y-(1-m)]2+m2+2m+1,讨论对称轴 y=1-m,得 函数f(x)的最大值g(m)的解析式.
(2)根据题意:t≤g(m)-m-2对任意的m∈[-4,0]恒成立,①当m∈[-4,-2)时,t≤-3m-5,可得t≤1.②当m∈[-2,0]时,t≤m2+m-1恒成立,求得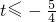 ,综合可得实数t的取值范围.
,综合可得实数t的取值范围.
点评:本题主要考查对数函数的值域,二次函数的性质应用以及函数的恒成立问题,属于中档题.
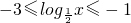 ,∴1≤log2x≤3,
,∴1≤log2x≤3,∵f(x)=(2m+log2x)(2-log2x),令log2x=y∈[1,3],
∴f(x)=(2m+y)(2-t)=-[y-(1-m)]2+m2+2m+1,…(4分)
讨论对称轴 y=1-m,得
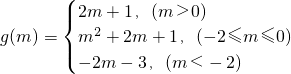 .…(10分)
.…(10分)(2)根据题意:t≤g(m)-m-2对任意的m∈[-4,0]恒成立,
①当m∈[-4,-2)时,t≤-3m-5,由于-3m-5关于m单调递减,∴t≤-3(-2)-5=1.…(12分)
②当m∈[-2,0]时,t≤m2+m-1,
而
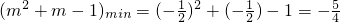 ,∴
,∴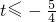 .…(15分)
.…(15分)综上,
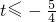 .…(16分)
.…(16分)分析:(1)令log2x=y∈[1,3],可得f(x)=(2m+y)(2-t)=-[y-(1-m)]2+m2+2m+1,讨论对称轴 y=1-m,得 函数f(x)的最大值g(m)的解析式.
(2)根据题意:t≤g(m)-m-2对任意的m∈[-4,0]恒成立,①当m∈[-4,-2)时,t≤-3m-5,可得t≤1.②当m∈[-2,0]时,t≤m2+m-1恒成立,求得
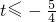 ,综合可得实数t的取值范围.
,综合可得实数t的取值范围.点评:本题主要考查对数函数的值域,二次函数的性质应用以及函数的恒成立问题,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
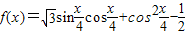 .
.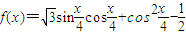 .
.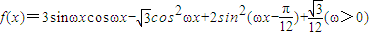 .
.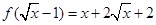 ,
,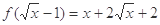 ,
,