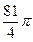题目内容
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知长方体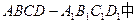 ,
, ,点M是棱
,点M是棱 的中点.
的中点.
(1)试用反证法证明 直线
直线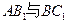 是异面直线;
是异面直线;
(2)求直线 所成的角(结果用反三角函数值表示).
所成的角(结果用反三角函数值表示).
已知长方体
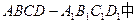 ,
, ,点M是棱
,点M是棱 的中点.
的中点.(1)试用反证法证明
 直线
直线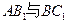 是异面直线;
是异面直线;(2)求直线
 所成的角(结果用反三角函数值表示).
所成的角(结果用反三角函数值表示).
略
证明 (1)(反证法)假设直线 与
与 不是异面直线. ……………………………1分
不是异面直线. ……………………………1分
设直线 与
与 都在平面
都在平面 上,则
上,则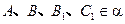 .………………………3分
.………………………3分
因此,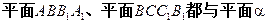 有不共线的三个公共点,即
有不共线的三个公共点,即
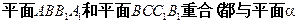 重合).又长方体的相邻两个面不重合,这是矛盾,于是,假设不成立. …………………………………………………………6分
重合).又长方体的相邻两个面不重合,这是矛盾,于是,假设不成立. …………………………………………………………6分
所以直线 与
与 是异面直线. …………………7分
是异面直线. …………………7分
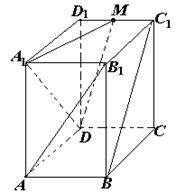
解 (2)按如图所示建立空间直角坐标系,可得有关点的坐标为D(0,0,0)、
A(4,0,0)、B(4,2,0),C(0,2,0), (4,0,4),
(4,0,4), (4,2,4),
(4,2,4),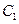 (0,2,4),
(0,2,4),
 (0,0,4).于是,M(0,1
(0,0,4).于是,M(0,1 ,4),
,4), …9分
…9分

设平面 的法向量为
的法向量为 ,则
,则
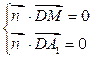 ,即
,即 .取
.取 . … 11分
. … 11分
所以平面 的一个法向量为
的一个法向量为 .
.
记直线 为
为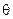 ,于是,
,于是,
 ,
, . ………………………13分
. ………………………13分
所以,直线 为
为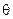 =
= .…………………14分
.…………………14分
 与
与 不是异面直线. ……………………………1分
不是异面直线. ……………………………1分设直线
 与
与 都在平面
都在平面 上,则
上,则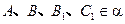 .………………………3分
.………………………3分因此,
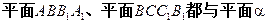 有不共线的三个公共点,即
有不共线的三个公共点,即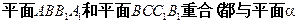 重合).又长方体的相邻两个面不重合,这是矛盾,于是,假设不成立. …………………………………………………………6分
重合).又长方体的相邻两个面不重合,这是矛盾,于是,假设不成立. …………………………………………………………6分所以直线
 与
与 是异面直线. …………………7分
是异面直线. …………………7分解 (2)按如图所示建立空间直角坐标系,可得有关点的坐标为D(0,0,0)、
A(4,0,0)、B(4,2,0),C(0,2,0),
 (4,0,4),
(4,0,4), (4,2,4),
(4,2,4),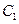 (0,2,4),
(0,2,4), (0,0,4).于是,M(0,1
(0,0,4).于是,M(0,1 ,4),
,4), …9分
…9分
设平面
 的法向量为
的法向量为 ,则
,则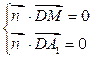 ,即
,即 .取
.取 . … 11分
. … 11分所以平面
 的一个法向量为
的一个法向量为 .
.记直线
 为
为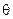 ,于是,
,于是, ,
, . ………………………13分
. ………………………13分所以,直线
 为
为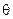 =
= .…………………14分
.…………………14分
练习册系列答案
相关题目
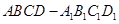 的各顶点都在半径为1的球面上,其中
的各顶点都在半径为1的球面上,其中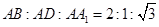 ,则两
,则两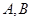 点的球面距离为( )
点的球面距离为( )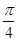
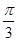
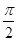
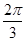
 的底面
的底面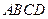 为一直角梯形,其中
为一直角梯形,其中
 ,
,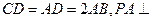 底面
底面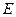 是
是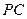 的中点.
的中点. //平面
//平面 ;
; 平面
平面 ,
, 与
与 所成角的余弦值;
所成角的余弦值;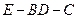 的余弦值.
的余弦值.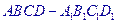 ,
,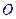 是底
是底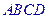 对角线的交点.
对角线的交点. 求证:
求证: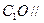 面
面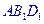 ;
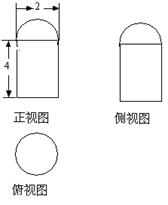
; 的正三棱柱的三视图如图所示,则这个三棱柱的左视图的面积为
的正三棱柱的三视图如图所示,则这个三棱柱的左视图的面积为
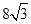


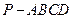 的顶点P在底面
的顶点P在底面


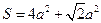
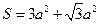
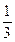 ,且
,且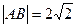 ,
, 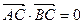 ,则球的表面积是( )
,则球的表面积是( )