题目内容
在△ABC中，
•
•
，则△ABC的形状为
- A.直角三角形
- B.等边三角形
- C.三边均不相等的三角形
- D.等腰非等边三角形
D
分析：依题意，∠A的角平分线与BC垂直，∠B≠
，从而可判断△ABC的形状．
解答：在△ABC中，∵（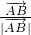
+
）•
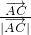=0，
∴∠A的角平分线AD与BC垂直，
∴△ABC为等腰三角形；
又
•
=1×1×cosB=
，
∴cosB=≠
，
∴∠B≠，
∴△ABC为等腰非等边三角形．
故选D．
点评：本题考查三角形的形状判断，考查平面向量数量积的含义，理解∠A的角平分线与BC垂直是关键，也是难点，属于中档题．
分析：依题意，∠A的角平分线与BC垂直，∠B≠
，从而可判断△ABC的形状．解答：在△ABC中，∵（
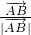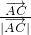+）•=0，∴∠A的角平分线AD与BC垂直，
∴△ABC为等腰三角形；
又
•=1×1×cosB=，∴cosB=
≠，∴∠B≠
，∴△ABC为等腰非等边三角形．
故选D．
点评：本题考查三角形的形状判断，考查平面向量数量积的含义，理解∠A的角平分线与BC垂直是关键，也是难点，属于中档题．
练习册系列答案
习题精选系列答案
相关题目