题目内容
(1)已知tanx=-2,求下列各式的值:①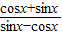 ;②2sin2x-3cos2x.
;②2sin2x-3cos2x.(2)求值:sin(-1071°)sin99°+sin(-171°)sin(-261°)-2sin(-420°)+tan(-330°).
【答案】分析:(1)把已知tanx=-2代入 ① =
= ,运算求得结果.把已知tanx=-2代入 ②2sin2x-3cos2x=
,运算求得结果.把已知tanx=-2代入 ②2sin2x-3cos2x= =
= ,运算求得结果.
,运算求得结果.
(2)利用诱导公式把要求的式子化为sin9°cos9°-sin9°sin99°+2sin60°+tan30°,运算求得结果.
解答:解:(1)∵已知tanx=-2,∴① =
= =
= =
= ,
,
②2sin2x-3cos2x= =
= =
= =1.
=1.
(2)sin(-1071°)sin99°+sin(-171°)sin(-261°)-2sin(-420°)+tan(-330°)
=sin(-3×360°+9°)cos9°+sin(9°-180°)sin(-360°+99°)-2sin(-360°-60°)+tan(-360°+30°)
=sin9°cos9°-sin9°sin99°+2sin60°+tan30°=2sin60°+tan30°= +
+ =
= .
.
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,属于中档题.
 =
= ,运算求得结果.把已知tanx=-2代入 ②2sin2x-3cos2x=
,运算求得结果.把已知tanx=-2代入 ②2sin2x-3cos2x= =
= ,运算求得结果.
,运算求得结果.(2)利用诱导公式把要求的式子化为sin9°cos9°-sin9°sin99°+2sin60°+tan30°,运算求得结果.
解答:解:(1)∵已知tanx=-2,∴①
 =
= =
= =
= ,
,②2sin2x-3cos2x=
 =
= =
= =1.
=1.(2)sin(-1071°)sin99°+sin(-171°)sin(-261°)-2sin(-420°)+tan(-330°)
=sin(-3×360°+9°)cos9°+sin(9°-180°)sin(-360°+99°)-2sin(-360°-60°)+tan(-360°+30°)
=sin9°cos9°-sin9°sin99°+2sin60°+tan30°=2sin60°+tan30°=
 +
+ =
= .
.点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
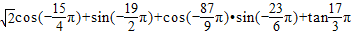 .
.