题目内容
已知条件p：x＞1，q：
＜1，则p是q的（ ）
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分必要条件的定义，分别证明其充分性和必要性，从而得到答案．
解答：
解：由x＞1，推出
＜1，p是q的充分条件，
由
＜1，得
＜0，解得：x＜0或x＞1．不是必要条件，
故选：A．
| 1 |
| x |
由
| 1 |
| x |
| 1-x |
| x |
故选：A．
点评：本题考查了充分必要条件，考查了不等式的解法，是一道基础题．
练习册系列答案
新思维寒假作业系列答案
相关题目
如图，正六边形ABCDEF中，
+
+
=（ ）
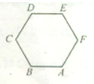
| BA |
| CD |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=sin(
-2x)是（ ）
| 5π |
| 2 |
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、以上都不对 |
偶函数f（x）在区间[-2，-1]上单调递减，则函数f（x）在区间[1，2]上（ ）
| A、单调递增，且有最小值f（1） |
| B、单调递增，且有最大值f（1） |
| C、单调递减，且有最小值f（2） |
| D、单调递减，且有最大值f（2） |