题目内容
（本大题12分）用反证法证明：若
．
．
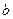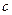
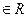，且
，
，
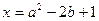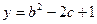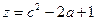，则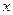
．
．
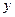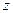中至少有一个不小于0．
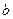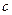
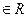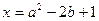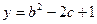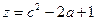．．，且，，，则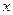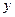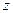．．中至少有一个不小于0．证明：假设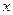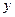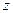．．均小于0，即：
①
②
③…………………………………6分
①+②+③得
，这与
矛盾，
则假设不成立，
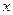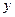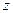∴．．中至少有一个不小于0．………………………………12分
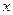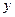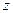．．均小于0，即：① ② ③…………………………………6分①+②+③得
，这与矛盾， 则假设不成立，
∴
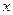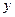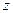．．中至少有一个不小于0．………………………………12分略
练习册系列答案
阅读快车系列答案
相关题目
在区间（4，+∞）上单调递增；q:loga2＜1，如果“┐p”是真命题，q也是真命题，求实数a的取值范围.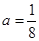
”是“对任意的正数
，
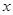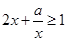”的 ( )
，
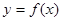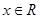，有下列4个命题：
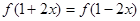，则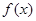
的图象关于直线
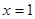对称；
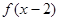与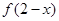
的图象关于直线
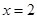对称；
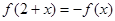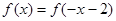，则
，则
，下列命题中正确的是（ ）
”的否定是 ▲ ．
,
一元二次方程
有正数根的充要条件是
= . 
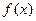是定义在R上的偶函数，且对任意的
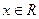恒有
，
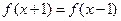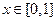时，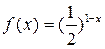
，则其中所有正确命题的序号
是_____________。
① 2是函数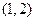
上是减函数，在
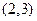上是增函数；
最
大值是1，最小值是0；④当
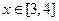时，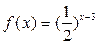
。