题目内容
已知函数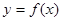 ,
,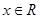 ,有下列4个命题:
,有下列4个命题:
①若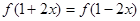 ,则
,则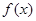 的图象关于直线
的图象关于直线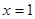 对称;
对称;
②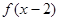 与
与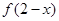 的图象关于直线
的图象关于直线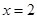 对称;
对称;
③若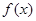 为偶函数,且
为偶函数,且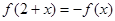 ,则
,则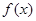 的图象关于直线
的图象关于直线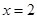 对称;
对称;
④若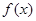 为奇函数,且
为奇函数,且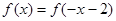 ,则
,则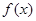 的图象关于直线
的图象关于直线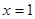 对称.
对称.
其中正确命题的个数为 ( ).
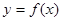 ,
,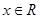 ,有下列4个命题:
,有下列4个命题:①若
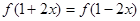 ,则
,则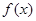 的图象关于直线
的图象关于直线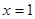 对称;
对称;②
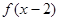 与
与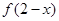 的图象关于直线
的图象关于直线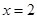 对称;
对称;③若
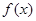 为偶函数,且
为偶函数,且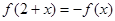 ,则
,则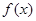 的图象关于直线
的图象关于直线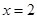 对称;
对称;④若
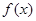 为奇函数,且
为奇函数,且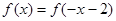 ,则
,则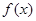 的图象关于直线
的图象关于直线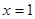 对称.
对称.其中正确命题的个数为 ( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解:①令t=1+2x,可得2x=t-1,代入f(1+2x)=f(1-2x)得f(t )=f(2-t)
由于|t-1|=|2-t-1|,故可知函数y=f(x)图象关于直线x=1对称
即y=f(x)的图象关于直线x=1对称,故①是真命题.
②由题设知y=f(2-x)=f[-(x-2)]
由于函数y=f(x)与y=f(-x)的图象关于直线x=0对称,
又y=f(x-2)与y=f(2-x)的图象可由函数y=f(x)与y=f(-x)的图象右移动2个单位而得到,
∴y=f(x-2)与y=f(2-x)的图象关于直线x=2对称,故②是真命题.
③f(x)为偶函数,且f(2+x)=-f(x),用-x换x得,f(2-x)=-f(-x)=-f(x)=f(2+x)
∴f(x)的图象关于直线x=2对称,故③是真命题.
④∵y=f(x)为奇函数,且f(x)=f(-x-2),用-x换x得,f(-x)=f(x-2),
∴y=f(x)的图象关于直线x=-1对称,故④是假命题.
故选C.
由于|t-1|=|2-t-1|,故可知函数y=f(x)图象关于直线x=1对称
即y=f(x)的图象关于直线x=1对称,故①是真命题.
②由题设知y=f(2-x)=f[-(x-2)]
由于函数y=f(x)与y=f(-x)的图象关于直线x=0对称,
又y=f(x-2)与y=f(2-x)的图象可由函数y=f(x)与y=f(-x)的图象右移动2个单位而得到,
∴y=f(x-2)与y=f(2-x)的图象关于直线x=2对称,故②是真命题.
③f(x)为偶函数,且f(2+x)=-f(x),用-x换x得,f(2-x)=-f(-x)=-f(x)=f(2+x)
∴f(x)的图象关于直线x=2对称,故③是真命题.
④∵y=f(x)为奇函数,且f(x)=f(-x-2),用-x换x得,f(-x)=f(x-2),
∴y=f(x)的图象关于直线x=-1对称,故④是假命题.
故选C.

练习册系列答案
相关题目
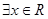 ,使得
,使得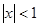 ”的否定是( )
”的否定是( )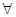 x
x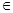 R,都有
R,都有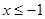 或
或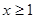
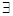 x
x
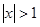
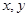 都是奇数,则
都是奇数,则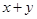 是偶数”,在它的逆命题,否命题,逆否命题中真命题有( )个
是偶数”,在它的逆命题,否命题,逆否命题中真命题有( )个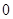
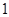
 .
. .
.
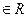 ,且
,且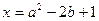 ,
,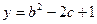 ,
,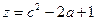 ,则
,则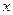 .
.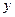 .
.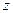 中至少有一个不小于0.
中至少有一个不小于0.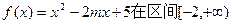 上是增函数 命题q:
上是增函数 命题q: 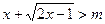 恒成立。若p或q为真命题,命题p且q为假,
恒成立。若p或q为真命题,命题p且q为假,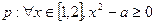 ,命题
,命题
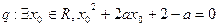 ,
,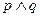 是真命题,求实数a的取值范围.
是真命题,求实数a的取值范围.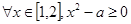 ,命题Q:
,命题Q: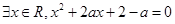
 若 “P且Q"为真命题,则实数
若 “P且Q"为真命题,则实数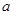 的取值范围是( )
的取值范围是( )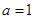 或
或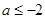 B.
B.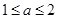 C.
C.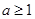 D.
D.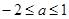
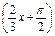 是奇函数;
是奇函数;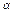 ,使得sin
,使得sin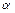 +cos
+cos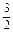 ;
;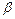 是第一象限角且
是第一象限角且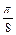 是函数y=sin
是函数y=sin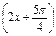 的一条对称轴方程;
的一条对称轴方程;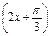 的图象关于点
的图象关于点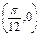 成中心对称图形.
成中心对称图形.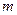 、
、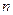 是两条不同的直线,
是两条不同的直线,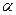 、
、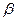 、
、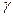 是三个不同的平面,给出下列四个命题:①若
是三个不同的平面,给出下列四个命题:①若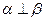 ,
,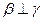 ,则
,则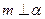 ,则
,则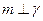 ;
;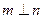 .其中正确命题的序号是 .
.其中正确命题的序号是 .