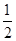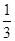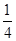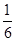题目内容
已知数列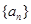 的首项
的首项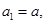 其中
其中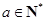 ,
,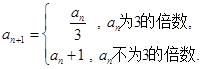 令集合
令集合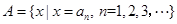 .
.
(Ⅰ)若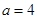 ,写出集合
,写出集合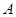 中的所有的元素;
中的所有的元素;
(Ⅱ)若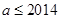 ,且数列
,且数列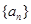 中恰好存在连续的7项构成等比数列,求
中恰好存在连续的7项构成等比数列,求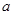 的所有可能取值构成的集合;
的所有可能取值构成的集合;
(Ⅲ)求证: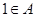 .
.
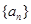 的首项
的首项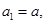 其中
其中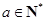 ,
,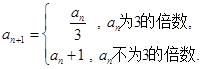 令集合
令集合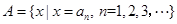 .
.(Ⅰ)若
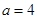 ,写出集合
,写出集合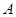 中的所有的元素;
中的所有的元素;(Ⅱ)若
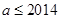 ,且数列
,且数列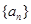 中恰好存在连续的7项构成等比数列,求
中恰好存在连续的7项构成等比数列,求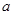 的所有可能取值构成的集合;
的所有可能取值构成的集合;(Ⅲ)求证:
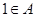 .
.(Ⅰ)集合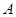 的所有元素为:4,5,6,2,3,1.
的所有元素为:4,5,6,2,3,1.
(Ⅱ)首项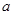 的所有可能取值的集合为{
的所有可能取值的集合为{ ,
,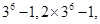
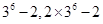 }.
}.
(Ⅲ)见解析.
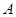 的所有元素为:4,5,6,2,3,1.
的所有元素为:4,5,6,2,3,1.(Ⅱ)首项
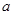 的所有可能取值的集合为{
的所有可能取值的集合为{ ,
,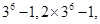
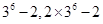 }.
}. (Ⅲ)见解析.
试题分析:(Ⅰ)将

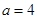 代入,依次写出集合
代入,依次写出集合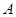 的所有元素.
的所有元素.(Ⅱ)不妨设成等比数列的这连续7项的第一项为
 ,关键是理解好“如果
,关键是理解好“如果 是3的倍数,则
是3的倍数,则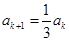 ;如果
;如果 是被3除余1,则由递推关系可得
是被3除余1,则由递推关系可得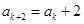 ,所以
,所以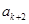 是3的倍数,所以
是3的倍数,所以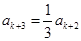 ;如果
;如果 被3除余2,则由递推关系可得
被3除余2,则由递推关系可得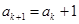 ,所以
,所以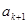 是3的倍数,所以
是3的倍数,所以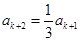 .”得到结论:该7项的等比数列的公比为
.”得到结论:该7项的等比数列的公比为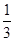 .
.(Ⅲ)分“
 被3除余1,
被3除余1, 被3除余2,,
被3除余2,, 被3除余0”加以讨论,确定得到
被3除余0”加以讨论,确定得到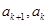 的关系为:
的关系为: ,
,从而利用
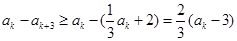
进一步得到
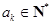 ,所以
,所以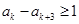 .数列
.数列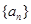 中必存在某一项
中必存在某一项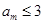 (否则会与上述结论矛盾!)
(否则会与上述结论矛盾!)并对
 ,
,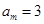 ,加以讨论,得到
,加以讨论,得到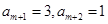 ,
,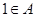 .
. 此题较难,对考生逻辑思维能力要求较高
试题解析:(Ⅰ)集合
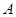 的所有元素为:4,5,6,2,3,1.. 3分
的所有元素为:4,5,6,2,3,1.. 3分(Ⅱ)不妨设成等比数列的这连续7项的第一项为
 ,
,如果
 是3的倍数,则
是3的倍数,则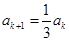 ;如果
;如果 是被3除余1,则由递推关系可得
是被3除余1,则由递推关系可得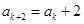 ,所以
,所以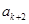 是3的倍数,所以
是3的倍数,所以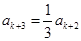 ;如果
;如果 被3除余2,则由递推关系可得
被3除余2,则由递推关系可得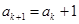 ,所以
,所以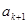 是3的倍数,所以
是3的倍数,所以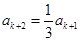 .
.所以,该7项的等比数列的公比为
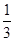 .
.又因为
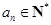 ,所以这7项中前6项一定都是3的倍数,而第7项一定不是3的倍数(否则构成等比数列的连续项数会多于7项),
,所以这7项中前6项一定都是3的倍数,而第7项一定不是3的倍数(否则构成等比数列的连续项数会多于7项),设第7项为
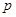 ,则
,则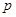 是被3除余1或余2的正整数,则可推得
是被3除余1或余2的正整数,则可推得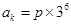
因为
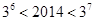 ,所以
,所以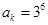 或
或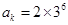 .
.由递推关系式可知,在该数列的前
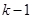 项中,满足小于2014的各项只有:
项中,满足小于2014的各项只有:
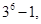 或
或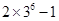 ,
,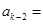
 或
或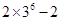 ,
,所以首项
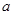 的所有可能取值的集合为
的所有可能取值的集合为{
 ,
,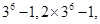
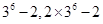 }. 8分
}. 8分(Ⅲ)若
 被3除余1,则由已知可得
被3除余1,则由已知可得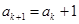 ,
,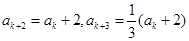 ;
;若
 被3除余2,则由已知可得
被3除余2,则由已知可得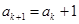 ,
,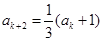 ,
,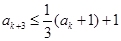 ;
;若
 被3除余0,则由已知可得
被3除余0,则由已知可得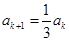 ,
, ;
;所以
 ,
,所以
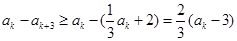
所以,对于数列
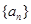 中的任意一项
中的任意一项 ,“若
,“若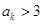 ,则
,则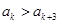 ”.
”.因为
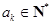 ,所以
,所以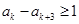 .
.所以数列
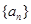 中必存在某一项
中必存在某一项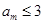 (否则会与上述结论矛盾!)
(否则会与上述结论矛盾!)若
 ,结论得证.
,结论得证.若
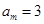 ,则
,则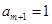 ;若
;若 ,则
,则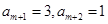 ,
,所以
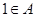 . 13分
. 13分
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
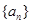 是公比大于1的等比数列,
是公比大于1的等比数列,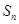 为其前
为其前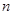 项和已知
项和已知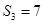 ,且
,且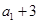 ,
,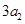 ,
,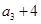 构成等差数列.
构成等差数列.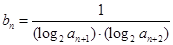 ,求数列
,求数列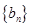 的前
的前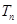 .
.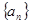 满足
满足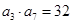 ,
,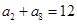 ,且
,且 (
(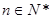 ).
).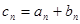 ,求数列
,求数列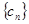 的前n项和
的前n项和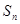 .
.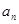 }的前n项和为
}的前n项和为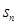 ,若
,若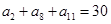 ,那么
,那么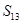 = .
= .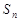 是等差数列
是等差数列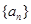 的前n项和,已知
的前n项和,已知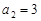 ,
,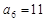 ,则
,则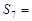 .
.
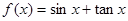 .项数为27的等差数列
.项数为27的等差数列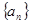 满足
满足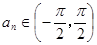 ,且公差
,且公差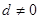 .若
.若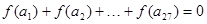 ,则当
,则当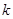 =____________时,
=____________时,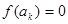 .
.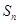 是公差不为0的等差数列
是公差不为0的等差数列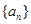 的前
的前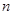 项和,若
项和,若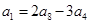 ,则
,则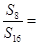 ( )
( )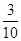
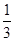
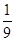
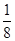
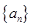 中,
中,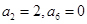 且数列
且数列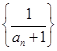 是等差数列,则
是等差数列,则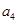 =( )
=( )