题目内容
如图,已知椭圆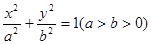 的左、右准线分别为
的左、右准线分别为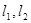 ,且分别交
,且分别交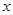 轴于
轴于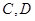 两点,从
两点,从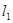 上一点
上一点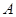 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点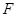 被
被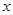 轴反射后与
轴反射后与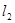 交于点
交于点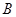 ,若
,若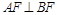 ,且
,且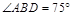 ,则椭圆的离心率等于 .
,则椭圆的离心率等于 .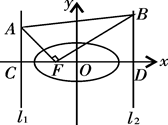
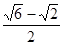 .
.
解析试题分析:由题意知|AC|=|CF|=-c-(-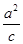 )=
)=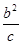 ,
,
∴|AF|=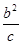
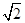 ,|BF|=
,|BF|=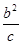
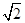 •cot30°=
•cot30°=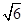
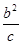 .
.
∵|BD|=|DF|=c+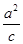 ,∴|BF|=
,∴|BF|=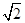 (c+
(c+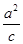 )=
)=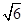
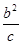 ,
,
∴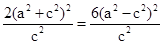 ,整理得e4-4e2+1=0.
,整理得e4-4e2+1=0.
解得e2=2-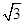 或e2=2+
或e2=2+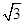 (舍去),
(舍去),
∴e=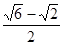 。
。
考点:本题主要考查椭圆的几何性质。
点评:典型题,椭圆的几何性质是重要考点之一,常常将a,b,c,e关系与椭圆的标准方程结合在一起进行考查。本题利用函数方程思想,通过建立e的方程,达到解题目的。

练习册系列答案
相关题目
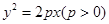 的焦点为
的焦点为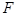 ,点
,点 在抛物线上,且
在抛物线上,且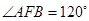 ,过弦
,过弦 中点
中点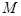 作准线
作准线 的垂线,垂足为
的垂线,垂足为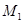 ,则
,则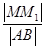 的最大值为_________.
的最大值为_________.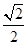 .过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为__________.
.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为__________.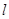 经过椭圆
经过椭圆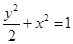 的焦点并且与椭圆相交于
的焦点并且与椭圆相交于 ,
,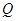 两点,线段
两点,线段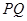 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点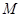 ,则
,则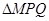 面积的最大值为 .
面积的最大值为 .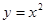 在点 处的切线平行于直线
在点 处的切线平行于直线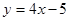 。
。 是抛物线
是抛物线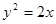 上的动点,点
上的动点,点 轴上的射影是
轴上的射影是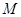 ,
,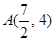 ,则
,则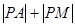 的最小值是 .
的最小值是 .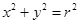 上任意一点
上任意一点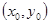 处的切线方程为:
处的切线方程为: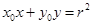 。类比以上结论有:双曲线:
。类比以上结论有:双曲线: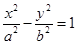 上任意一点
上任意一点