题目内容
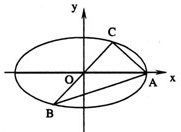
已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个顶点，BC过椭圆中心O，如图，且
•
=0，|BC|=2|AC|．
（1）求椭圆的方程；
（2）如果椭圆上两点P、Q使∠PCQ的平分线垂直AO，则总存在实数λ，使
=λ
，请给出证明．
| AC |
| BC |
（1）求椭圆的方程；
（2）如果椭圆上两点P、Q使∠PCQ的平分线垂直AO，则总存在实数λ，使
| PQ |
| AB |
（1）以O为原点，OA所在的直线为x轴建立如图所示的直角坐标系，
则A（2，0），设所求椭圆的方程为：x2+
=4（0＜b＜1），由椭圆的对称性知|OC|=|OB|，
由
•
=0得AC⊥BC，
∵|BC|=2|AC|，
∴|OC|=|AC|，
∴△AOC是等腰直角三角形，
∴C的坐标为（1，1），
∵C点在椭圆上
∴1+
=4，
∴b2=
，所求的椭圆方程为x2+3y2=4．
（Ⅱ）由于∠PCQ的平分线垂直OA（即垂直于x轴），
不妨设直线PC的斜率为k，则直线QC的斜率为-k，
直线PC的方程为：y=k（x-1）+1，直线QC的方程为y=-k（x-1）+1，
由
得：（1+3k2）x2-6k（k-1）x+3k2-6k-1=0（*）
∵点C（1，1）在椭圆上，
∴x=1是方程（*）的一个根，则其另一根为
，设P（xP，yP），?Q（xQ，yQ），xP=
，同理xQ=
，
kPQ=
=
=
=
而由对称性知B（-1，-1），又A（2，0），
∴kAB=
，
∴kPQ=kAB，
∴
与
共线，且
≠0，即存在实数λ，使
=λ
．
则A（2，0），设所求椭圆的方程为：x2+
| y2 |
| b2 |
由
| AC |
| BC |
∵|BC|=2|AC|，
∴|OC|=|AC|，
∴△AOC是等腰直角三角形，
∴C的坐标为（1，1），
∵C点在椭圆上
∴1+
| 1 |
| b2 |
∴b2=
| 1 |
| 3 |
（Ⅱ）由于∠PCQ的平分线垂直OA（即垂直于x轴），
不妨设直线PC的斜率为k，则直线QC的斜率为-k，
直线PC的方程为：y=k（x-1）+1，直线QC的方程为y=-k（x-1）+1，
由
|
∵点C（1，1）在椭圆上，
∴x=1是方程（*）的一个根，则其另一根为
| 3k2-6k-1 |
| 1+3k2 |
| 3k2-6k-1 |
| 1+3k2 |
| 3k2+6k-1 |
| 1+3k2 |
kPQ=
| yp-yQ |
| xP-xQ |
| k(xP+xQ)-2k |
| xP-xQ |
k(
| ||||
|
| 1 |
| 3 |
而由对称性知B（-1，-1），又A（2，0），
∴kAB=
| 1 |
| 3 |
∴kPQ=kAB，
∴
| AB |
| PQ |
| AB |
| PQ |
| AB |
练习册系列答案
名校课堂系列答案
相关题目
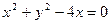外切，且与y轴相切的动圆圆心的轨迹方程为 .
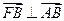时,其离心率为
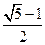,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲ 
