题目内容
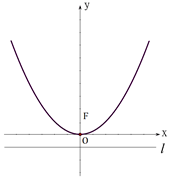
如图,抛物线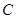 的顶点为坐标原点
的顶点为坐标原点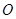 ,焦点
,焦点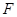 在
在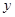 轴上,准线
轴上,准线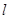 与圆
与圆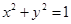 相切.
相切.
(Ⅰ)求抛物线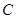 的方程;
的方程;
(Ⅱ)已知直线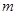 和抛物线
和抛物线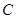 交于点
交于点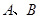 ,命题P:“若直线
,命题P:“若直线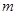 过定点
过定点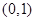 ,则
,则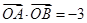 ”,请判断命题P的真假,并证明。
”,请判断命题P的真假,并证明。
 的顶点为坐标原点
的顶点为坐标原点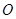 ,焦点
,焦点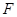 在
在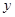 轴上,准线
轴上,准线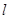 与圆
与圆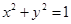 相切.
相切.
(Ⅰ)求抛物线
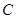 的方程;
的方程;(Ⅱ)已知直线
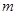 和抛物线
和抛物线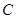 交于点
交于点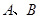 ,命题P:“若直线
,命题P:“若直线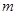 过定点
过定点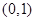 ,则
,则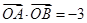 ”,请判断命题P的真假,并证明。
”,请判断命题P的真假,并证明。(Ⅰ)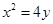 (Ⅱ)命题P为真命题
(Ⅱ)命题P为真命题
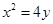 (Ⅱ)命题P为真命题
(Ⅱ)命题P为真命题试题分析:(Ⅰ)依题意,可设抛物线
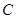 的方程为
的方程为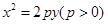 ,
,其准线
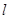 的方程为
的方程为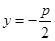 .
. ∵准线
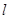 与圆
与圆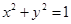 相切,
相切,∴所以圆心
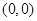 到直线
到直线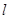 的距离
的距离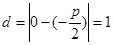 ,解得
,解得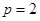 .
. 故抛物线
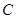 的方程为:
的方程为: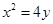 .
. (Ⅱ)命题P为真命题
因为直线
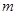 和抛物线
和抛物线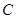 交于点
交于点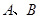 且过定点
且过定点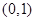 ,所以直线
,所以直线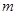 的斜率
的斜率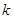 一定存在
一定存在设直线
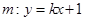 ,交点
,交点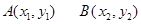 联立抛物线
联立抛物线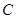 的方程
的方程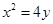 ,
,得
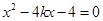
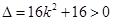 恒成立
恒成立 由韦达定理得

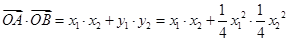
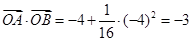 ,所以命题P为真命题
,所以命题P为真命题 点评:本题考查了抛物线方程的求法,以及直线与抛物线的位置关系判断,做题时要认真分析,避免不必要的错误.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
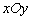 有相同的长度单位,以原点
有相同的长度单位,以原点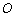 为极点,以
为极点,以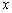 正半轴为极轴,已知曲线
正半轴为极轴,已知曲线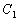 的极坐标方程为
的极坐标方程为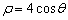 ,曲线
,曲线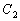 的参数方程是
的参数方程是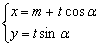 (
(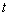 为参数,
为参数,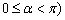 ,射线
,射线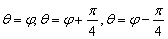 与曲线
与曲线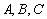
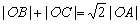 ;
;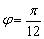 时,
时,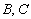 两点在曲线
两点在曲线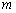 与
与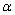 的值.
的值.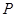 是双曲线
是双曲线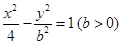 上一点,
上一点,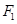 、
、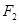 是其左、右焦点,
是其左、右焦点,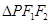 的三边长成等差数列,且
的三边长成等差数列,且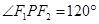 ,则双曲线的离心率等于
,则双曲线的离心率等于
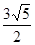
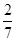
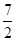
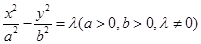 同一条渐近线上的两个不同的点,已知向量
同一条渐近线上的两个不同的点,已知向量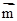 =(1,0),
=(1,0),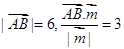 ,则双曲线的离心率e等于
,则双曲线的离心率e等于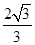 C.2或
C.2或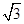 D. 2或
D. 2或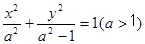 的左右焦点为
的左右焦点为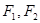 ,抛物线C:
,抛物线C: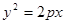 以F2为焦点且与椭圆相交于点
以F2为焦点且与椭圆相交于点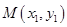 、
、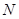
 ,点
,点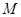 在
在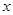 轴上方,直线
轴上方,直线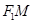 与抛物线
与抛物线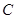 相切.
相切.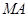 ,
,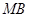 与
与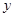 轴分别交于点
轴分别交于点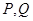 .
. 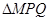 是以
是以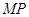 ,
,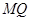 为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.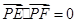 ,由点P向x轴作垂线段PQ,垂足为Q,点M满足
,由点P向x轴作垂线段PQ,垂足为Q,点M满足 ,点M的轨迹为C.
,点M的轨迹为C.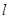 与曲线C交于A、B两点,点N满足
与曲线C交于A、B两点,点N满足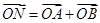
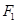 ,
,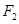 是椭圆
是椭圆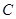 的两个焦点,焦距为4.若
的两个焦点,焦距为4.若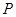 为椭圆
为椭圆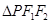 的周长为14,则椭圆
的周长为14,则椭圆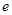 为______________
为______________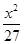 +
+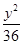 =1有公共的焦点,且与椭圆相交,它们的交点中一个交点的纵坐标是4,求双曲线的标准方程。
=1有公共的焦点,且与椭圆相交,它们的交点中一个交点的纵坐标是4,求双曲线的标准方程。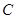 :
: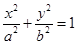
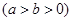 的离心率为
的离心率为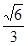 ,过右焦点
,过右焦点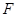 且斜率为
且斜率为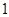 的直线交椭圆
的直线交椭圆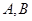 两点,
两点,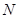 为弦
为弦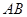 的中点,
的中点,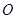 为坐标原点.
为坐标原点.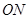 的斜率
的斜率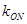 ;
;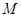 ,都存在
,都存在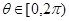 ,使得
,使得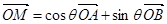 成立.
成立.