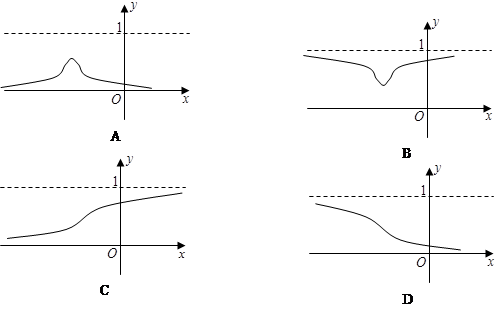题目内容
已知椭圆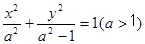 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: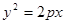 以F2为焦点且与椭圆相交于点
以F2为焦点且与椭圆相交于点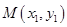 、
、
 ,点
,点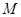 在
在 轴上方,直线
轴上方,直线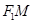 与抛物线
与抛物线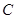 相切.
相切.
(1)求抛物线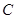 的方程和点
的方程和点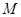 、
、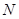 的坐标;
的坐标;
(2)设A,B是抛物线C上两动点,如果直线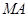 ,
,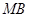 与
与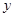 轴分别交于点
轴分别交于点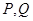 .
. 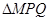 是以
是以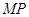 ,
,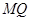 为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
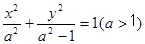 的左右焦点为
的左右焦点为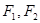 ,抛物线C:
,抛物线C: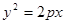 以F2为焦点且与椭圆相交于点
以F2为焦点且与椭圆相交于点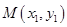 、
、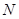
 ,点
,点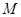 在
在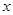 轴上方,直线
轴上方,直线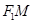 与抛物线
与抛物线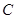 相切.
相切.(1)求抛物线
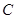 的方程和点
的方程和点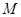 、
、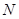 的坐标;
的坐标;(2)设A,B是抛物线C上两动点,如果直线
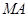 ,
,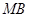 与
与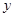 轴分别交于点
轴分别交于点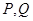 .
. 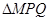 是以
是以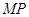 ,
,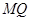 为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.(1)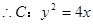 M、N的坐标分别为(1,2)、(1,-2)。
M、N的坐标分别为(1,2)、(1,-2)。
(2)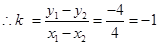 为定值
为定值
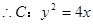 M、N的坐标分别为(1,2)、(1,-2)。
M、N的坐标分别为(1,2)、(1,-2)。(2)
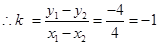 为定值
为定值试题分析:解:(1)由椭圆方程得半焦距
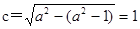 1分
1分所以椭圆焦点为
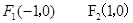
又抛物线C的焦点为
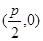
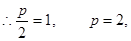
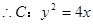 3分
3分∵
 在抛物线C上,
在抛物线C上,∴
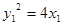 ,直线
,直线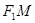 的方程为
的方程为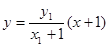 4分
4分代入抛物线C得
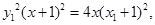
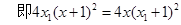
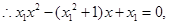 5分
5分∵
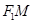 与抛物线C相切,
与抛物线C相切,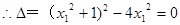 , 6分
, 6分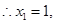 ∴ M、N的坐标分别为(1,2)、(1,-2)。 7分
∴ M、N的坐标分别为(1,2)、(1,-2)。 7分(2)直线AB的斜率为定值—1.
证明如下:设
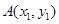 ,
,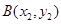 ,
,
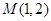 ,A、B在抛物线
,A、B在抛物线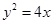 上,
上,
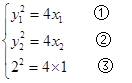
由①-③得,

由②-③得,
 10分
10分因为
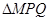 是以MP,MQ为腰的等腰三角形,所以
是以MP,MQ为腰的等腰三角形,所以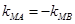 10分
10分由
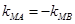 得
得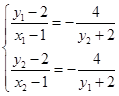 化简整理,
化简整理,得
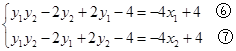
由
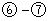 得:
得: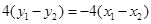
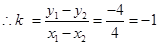 为定值 14分
为定值 14分解法二:设
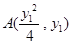 ,
,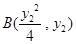 6分
6分则
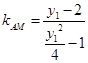
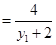 ,
,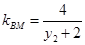 8分
8分因为
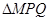 是以MP,MQ为腰的等腰三角形,所以
是以MP,MQ为腰的等腰三角形,所以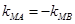 10分
10分即

所以
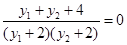
所以,由
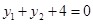 得
得 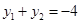 12分
12分所以,
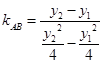
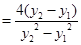
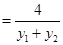

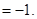
所以,直线AB的斜率为定值,这个定值为
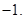 14分
14分点评:主要是考查了抛物线方程的方程的求解以及直线与抛物线的位置关系的运用,属于中档题。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
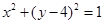 ,曲线C2:
,曲线C2: ,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则
,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则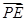 ·
·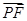 的最小值为 ( )
的最小值为 ( )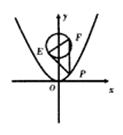
 的焦点F是椭圆
的焦点F是椭圆 的一个焦点,且它们的交点M到F的距离为
的一个焦点,且它们的交点M到F的距离为 ,则椭圆的离心率为
,则椭圆的离心率为



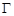 :
: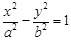
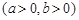 的离心率
的离心率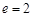 ,过双曲线
,过双曲线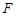 作
作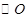 :
: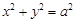 的两条切线,切点分别为
的两条切线,切点分别为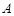 、
、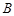 ,则
,则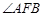 的大小等于( )
的大小等于( )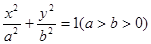 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=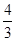 ,
,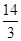 , PF1⊥F1F2.
, PF1⊥F1F2. 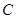 的顶点为坐标原点
的顶点为坐标原点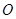 ,焦点
,焦点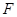 在
在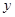 轴上,准线
轴上,准线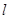 与圆
与圆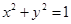 相切.
相切.
 和抛物线
和抛物线 ,命题P:“若直线
,命题P:“若直线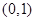 ,则
,则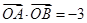 ”,请判断命题P的真假,并证明。
”,请判断命题P的真假,并证明。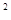 =4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=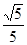
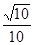
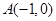 和
和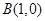 ,动点
,动点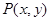 在直线
在直线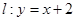 上移动,椭圆
上移动,椭圆 以
以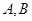 为焦点且经过点
为焦点且经过点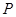 ,记椭圆
,记椭圆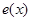 ,则函数
,则函数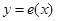 的大致图像是( )
的大致图像是( )