题目内容
3.已知平面α和β,在平面α内任取一条直线α,在β内总存在直线b∥a,则α与β的位置关系是平行(填“平行”或“相交”).分析 假设α∩β=l,当α中一条直线与l相交,且在β中不过这个交点的直线不满足b∥a,故假设不成立,由此得到α与β的位置关系是平行.
解答 解:假设α∩β=l,则在平面α内,与l相交的直线a,
设a∩l=A,
对β内的任意一直线b,若b过点A,则a与b相交,若b不过点A,则a,b异面,
即β内不存在直线b∥a,
这与在平面α内任取一条直线α,在β内总存在直线b∥a,相矛盾,故假设不成立,
∴α与β的位置关系是平行.
故答案为:平行.
点评 本题考查两直线的位置关系的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
13.集合A={x|y=log2(x+1)},B={-1,0,1},则A∩B等于( )
| A. | {0,1} | B. | {-1,0,1} | C. | {0} | D. | {1} |
12.函数f(x)=sin2(2x+$\frac{π}{3}$)的导数是( )
| A. | f′(x)=2sin(2x+$\frac{π}{3}$) | B. | f′(x)=4sin(2x+$\frac{π}{3}$) | C. | f′(x)=sin(4x+$\frac{2π}{3}$) | D. | f′(x)=2sin(4x+$\frac{2π}{3}$) |
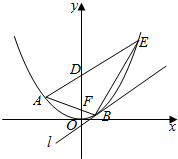 如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l
如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l