Question

【题目】现有一张半径为的圆形铁皮，从中裁剪出一块扇形铁皮（如图阴影部分），并卷成一个深度为的圆锥筒，如图.

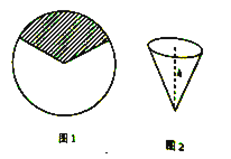
（1）若所裁剪的扇形铁皮的圆心角为，求圆锥筒的容积；

（2）当为多少时，圆锥筒的容积最大？并求出容积的最大值.

Answer 1

【答案】（1）；（2）当时，圆锥筒的容积的最大值为.

【解析】

（1）计算出扇形的弧长，利用扇形的弧长等于圆锥底面圆的周长可求出圆锥底面圆的半径，利用勾股定理计算出圆锥的高，再利用圆锥的体积公式可计算出圆锥的容积；

（2）利用勾股定理得出圆锥的底面半径为，可得出，利用圆锥的体积公式计算出圆锥的容积关于的函数，再利用导数可求出的最大值，并求出对应的的值.

设圆锥筒的半径为，容积为.

（1）由，得，从而，

所以.

答：圆锥筒的容积为；

（2）因为，.

所以，即，.

因为，令得，（舍负值），列表如下：

		极大值

所以，当时，取极大值即最大值，且的最大值为.

答：当时，圆锥筒的容积的最大值为.