题目内容
【题目】已知抛物线![]() 的内接等边三角形
的内接等边三角形![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)试求抛物线![]() 的方程;
的方程;
(2)已知点![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是以点
是以点![]() 为直角顶点的直角三角形.
为直角顶点的直角三角形.
①求证:直线![]() 恒过定点;
恒过定点;
②过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点
于点![]() ,试求点
,试求点![]() 的轨迹方程,并说明其轨迹是何种曲线.
的轨迹方程,并说明其轨迹是何种曲线.
【答案】(1)![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() ,是以
,是以![]() 为直径的圆(除去点
为直径的圆(除去点![]() .
.
【解析】
(1)设A(xA,yA),B(xB,yB),由|OA|=|OB|,可得![]() 2pxA
2pxA![]() 2pxB,化简可得:点A,B关于x轴对称.因此AB⊥x轴,且∠AOx=30°.可得yA=2
2pxB,化简可得:点A,B关于x轴对称.因此AB⊥x轴,且∠AOx=30°.可得yA=2![]() p,再利用等边三角形的面积计算公式即可得出;
p,再利用等边三角形的面积计算公式即可得出;
(2)①由题意可设直线PQ的方程为:x=my+a,P(x1,y1),Q(x2,y2).与抛物线方程联立化为:y2﹣my﹣a=0,利用∠PMQ=90°,可得![]() 0利用根与系数的关系可得
0利用根与系数的关系可得![]() m
m![]() ,或
,或![]() (m
(m![]() ),进而得出结论;
),进而得出结论;
②设N(x,y),根据MN⊥NH,可得![]() 0,即可得出.
0,即可得出.
(1)解依题意,设![]() ,
,![]() ,
,
则由![]() ,得
,得![]() ,
,
即![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
故![]() ,
,![]() ,
,
则![]() ,
,![]() 关于
关于![]() 轴对称,
轴对称,
所以![]() 轴,且
轴,且![]() ,
,
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
故![]() ,
,![]() ,
,
故抛物线![]() 的方程为
的方程为![]() .
.
(2)①证明 由题意可设直线![]() 的方程为
的方程为![]() ,
,
![]() ,
,![]() ,
,
由![]() ,消去
,消去![]() ,得
,得![]() ,
,
故![]() ,
,![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
即![]() .
.
整理得![]() ,
,
![]() ,
,
即![]() ,
,
得![]() ,
,
所以![]() 或
或![]() .
.
当![]() ,即
,即![]() 时,
时,
直线![]() 的方程为
的方程为![]() ,
,
过定点![]() ,不合题意舍去.
,不合题意舍去.
故直线![]() 恒过定点
恒过定点![]() .
.
②解 设![]() ,则
,则![]() ,即
,即![]() ,
,
得![]() ,
,
即![]() ,
,
即轨迹是以![]() 为直径的圆(除去点
为直径的圆(除去点![]() ).
).

【题目】某班主任对全班50名学生学习积极性和对待工作的态度进行了调查,统计数据如下所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法有多大把握认为学生的学习积极性与对班级工作的态度有关系?并说明理由.
本题参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
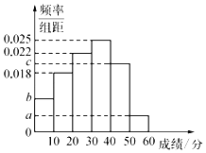
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: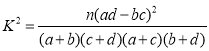 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |