题目内容
已知在x=-
时,函数g(x)=cos(2x+α)取得最小值,求使f(x)=sin(2x-α)的最大值的x的集合.
| π |
| 3 |
考点:三角函数的最值
专题:三角函数的求值
分析:由已知求出α,然后化简f(x),求最大值.
解答:
解:已知在x=-
时,函数g(x)=cos(2x+α)取得最小值,
所以g(
)=cos(2×
+α)=-1,所以α=2kπ+
,
所以f(x)=sin(2x-α)=sin(2x-2kπ-
)=sin(2x-
),
当2x-
=2kπ+
时,f(x)=sin(2x-α)的最大值为1,x的集合为{x|x=kπ+
,k∈Z}.
| π |
| 3 |
所以g(
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
所以f(x)=sin(2x-α)=sin(2x-2kπ-
| π |
| 3 |
| π |
| 3 |
当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
点评:本题考查了三角函数的最值求法以及对应的自变量集合,明确正弦函数和余弦函数的最值以及自变量范围是关键.

练习册系列答案
相关题目
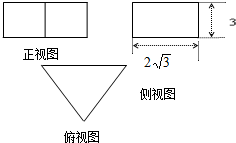 一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )
一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )A、4(9+2
| ||
B、(24+8
| ||
C、14
| ||
D、18
|
已知函数f(x)满足:①定义域为R;②?x∈R,有f(x+2)=f(x);③当x∈[0,2]时,f(x)=2|x-1|,设φ(x)=f(x)-
(x∈[-8,8])根据以上信息,可以得到函数φ(x)的零点个数为( )
| |x| |
| A、4 | B、5 | C、9 | D、8 |
 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分步和频率分布直方图
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分步和频率分布直方图