题目内容
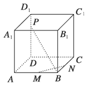
如图所示，M、N、P分别是正方体ABCD－A1B1C1D1的棱AB、BC、DD1上的点．
(1)若
＝
，求证：无论点P在DD1上如何移动，总有BP⊥MN；
(2)棱DD1上是否存在这样的点P，使得平面APC1⊥平面ACC1？证明你的结论．
(1)如图所示，连结B1M、B1N、AC、BD，则BD⊥AC.
∵＝，∴MN∥AC.
∴BD⊥MN.
∵DD1⊥平面ABCD，MN⊂面ABCD，∴DD1⊥MN.
∴MN⊥平面BDD1.
∵无论P在DD1上如何移动，总有BP⊂平面BDD1，故总有MN⊥BP.
(2)存在点P，且P为DD1的中点，使得平面APC1⊥平面ACC1.
∵BD⊥AC，BD⊥CC1，
∴BD⊥平面ACC1.
取BD1的中点E，连结PE，
则PE∥BD.∴PE⊥面ACC1.
又∵PE⊂面APC1，
∴面APC1⊥面ACC1.
练习册系列答案
全优点练单元计划系列答案
相关题目
如图所示，M，N是函数y=2sin（wx+φ）（ω＞0）图象与x轴的交点，
（2013•宁德模拟）已知函数f（x）=2sin（ωx+φ）（ω＞0，丨φ丨＜
中棱AB，BC，
，C
的中点．
＝
，求证：无论点P在DD1上如何移动，总有BP⊥MN；