题目内容
如图所示，M，N是函数y=2sin（wx+φ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时
| PM |
| PN |
（ ）
分析：由图形可以看出当P位于M、N之间函数y=2sin（wx+φ）（ω＞0）图象的最高点时，△MPN面最大，
再根据此时
•
=0得到△MPN为等腰直角三角形，由三角函数的最大值求出周期，然后利用周期公式求解ω的值．
再根据此时
| PM |
| PN |
解答：解：由图象可知，当P位于M、N之间函数y=2sin（wx+φ）（ω＞0）图象的最高点时，△MPN面积最大．
又此时
•
=0，
∴△MPN为等腰直角三角形，过P作PQ⊥x轴于Q，
∴|PQ|=2，
则|MN|=2|PQ|=4，
∴周期T=2|MN|=8．
∴ω=
=
=
．
故选A．
又此时
| PM |
| PN |
∴△MPN为等腰直角三角形，过P作PQ⊥x轴于Q，
∴|PQ|=2，
则|MN|=2|PQ|=4，
∴周期T=2|MN|=8．
∴ω=
| 2π |
| T |
| 2π |
| 8 |
| π |
| 4 |
故选A．
点评：本题考查了数量积判断两个向量的垂直关系，考查了y=Asin（ωx+φ）的图象，训练了三角函数周期公式的应用，是基础题．
练习册系列答案
相关题目
·
＝0，则ω＝
）（ω＞0）图像与x轴的交点，点P在M，N之间的图像上运动，当△MPN面积最大时
·
＝0，则ω＝ （ ）
B．
C．
D．8
（ω＞0）图像与x轴的交点，点P在M，N之间的图像上运动，当△MPN面积最大时
，则ω＝ （
）
B．
C．
D．8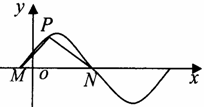
如图所示，M，N是函数y＝2sin（wx＋
）（ω＞0）图像与x轴的交点，点P在M，N
·
＝0，则ω＝ （ ）
B．
D．8