题目内容
已知：等比数列{an}的首项为a1，公比为q．
（1）写出数列{an}的前n项和Sn的公式；
（2）给出（1）中的公式的证明．
解：（1）
；
（2）由等比数列及其前n项和的定义知：
①
当q=1时，Sn=na1；
当q≠1时，把①式两边同乘q，得
②
由①-②，得
，∴
．
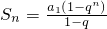综上：当q=1时，Sn=na1；当q≠1时，．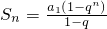
分析：（1）注意分公比q=1与q≠1两种情况写出即可；
（2）利用“错位相减法”即可证明．
点评：熟练掌握分类讨论的思想方法、“错位相减法”是解题的关键．
；（2）由等比数列及其前n项和的定义知：
①当q=1时，Sn=na1；
当q≠1时，把①式两边同乘q，得
②由①-②，得
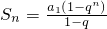，∴．综上：当q=1时，Sn=na1；当q≠1时，
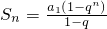．分析：（1）注意分公比q=1与q≠1两种情况写出即可；
（2）利用“错位相减法”即可证明．
点评：熟练掌握分类讨论的思想方法、“错位相减法”是解题的关键．
练习册系列答案
相关题目