题目内容
已知圆C:x2+y2+2x-4y+3=0.
(1)若不过原点的直线l与圆C相切,且在x轴,y轴上的截距相等,求直线l的方程;
(2)从圆C外一点P(x,y)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求点P的轨迹方程.
(1)由圆C:x2+y2+2x-4y+3=0,
得圆心坐标C(-1,2),半径r=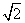 ,
,
∵切线在两坐标轴上的截距相等且不为零.
设直线l的方程为x+y=a,
∵直线l与圆C相切,
∴ =
=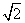 ,
,
∴a=-1或a=3.
∴所求直线l的方程为x+y+1=0或x+y-3=0.
(2)∵切线PM与半径CM垂直,设P(x,y),
又∵|PM|2=|PC|2-|CM|2,|PM|=|PO|,
∴(x+1)2+(y-2)2-2=x2+y2,
∴2x-4y+3=0,
∴所求点P的轨迹方程为2x-4y+3=0.

练习册系列答案
相关题目
 中,
中, ,且
,且 为
为 和
和 的等比中项,求数列
的等比中项,求数列 的首项、公差及前
的首项、公差及前 项和.
项和.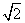 的圆C与直线y=x相切于坐标原点O.
的圆C与直线y=x相切于坐标原点O.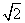 的圆C与直线y=x相切于坐标原点O.
的圆C与直线y=x相切于坐标原点O.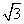 ,求l的方程;
,求l的方程;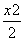 +y2=1 B.
+y2=1 B.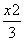 +
+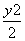 =1
=1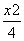 +
+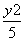 =1 D.
=1 D.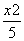 +
+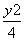 =1
=1 ,N为B1B的中点,则|
,N为B1B的中点,则| |为( )
|为( ) a B.
a B. a
a  a D.
a D. a
a