题目内容
已知椭圆
解:由直线l的方程与椭圆的方程可以知道,直线l与椭圆不相交.
设直线m平行于直线l,则直线m的方程可以写成4x-5y+k=0. ①
由方程组
消去y,得25x2+8kx+k2-225=0. ②
令方程②的根的判别式Δ=0,得
64k2-4×25(k2-225)=0. ③
解方程③得
k1=25,或k2=-25(不符合题意,舍去).
由图可知,当k=25时,直线m与椭圆的交点到直线l的距离最近,此时直线m的方程为4x-5y+25=0.

直线m与直线l间的距离d=![]() .
.
所以,所求最小距离是![]() .
.

练习册系列答案
相关题目
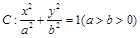 ,直线l为圆
,直线l为圆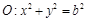 的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为
的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为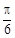 ,记椭圆C的离心率为e.
,记椭圆C的离心率为e.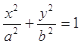
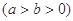 和直线L:
和直线L: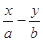 =1, 椭圆的离心率
=1, 椭圆的离心率 ,直线L与坐标原点的距离为
,直线L与坐标原点的距离为 。
。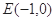 ,若直线
,若直线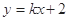
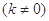 与椭圆相交于C、D两点,试判断是否存在
与椭圆相交于C、D两点,试判断是否存在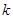 值,使以CD为直径的圆过定点E?若存在求出这个
值,使以CD为直径的圆过定点E?若存在求出这个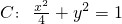 ,直线l与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点.
,直线l与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点.